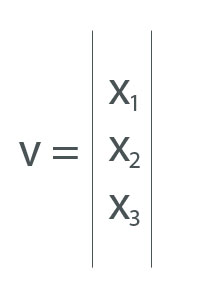Categoria: MatematicaMENTE FisicaMENTE LogicaMENTE

Allena la mente conoscendo meglio la matematica usando poi la maggiore elasticità mentale per migliorare la tua vita ed il tuo lavoro…

Pubblicato il

Matematicamente

Rispondendo a Mirco

Dunque tu hai trovato due vettori, uno indicato come segue se ho ben capito:

v=(x1, x2, x3)T

ed un altro indicato così:

matrice-colonna-o-vettore.jpg

Ti spiego subito:

per semplicità di scrittura, nei libri di scienza delle costruzioni (ma come vedi anche in un Blog è utile) si è soliti effettuare la trasposta del vettore ovvero della matrice colonna. Per trasposta si intende semplicemente lo scambio di righe con le colonne.

Nel caso specifico di una matrice ad una sola colonna, ovvero di un vettore, effettuare la trasposta implica la riscrittura dei termini, che descrivono il vettore, in orizzontale. In tal modo è più semplice scrivere un vettore sia su un libro che su un blog. Appena effettuata questa operazione si aggiunge un apice con la T (trasposta appunto).

Fai attenzione che nel caso di una matrice quadrata 3×3 ad esempio, per ottenere la trasposta devi scambiare la prima colonna con la prima riga, la seconda colonna con la seconda riga, la terza colonna con la terza riga, ecc.

Pubblicato il

Grandezze scalari – Grandezze vettoriali

Rubrica: Fisicamente
Titolo o argomento: Differenza tra grandezze scalari e vettoriali

 Sono grandezze scalari: il volume, la massa, la temperatura, il tempo, l’energia e tutte le grandezze che hanno un modulo (o intensità) ma non una direzione. Ad esempio 4 m3 il cui modulo è 4; oppure 75 kg il cui modulo è 75… ecc. Queste grandezze ci comunicano la loro intensità rispetto ad una scala di riferimento come quella della temperatura ad esempio.

 Sono grandezze vettoriali: lo spostamento di un corpo, la sua velocità; l’accelerazione, la forza, il campo elettrico, il campo magnetico. Ovvero quelle grandezze che vengono rappresentate dai vettori, cioè da segmenti orientati da una freccia che ne determina direzione e verso. La lunghezza del vettore determinata rispetto all’unità prefissata ne misura l’intensità (o modulo).

Esempi di vettori

Vedi anche: Articolo sulle simulazioni motoristiche

  • spostamento

vettore-posizione.jpg

  • velocità

vettore-velocita.jpg

  • accelerazione
  • forza

vettore-forza-vettore-accelerazione.jpg

vettori-live-for-speed.jpg

Pubblicato il

Rovina del giocatore d’azzardo

Rubrica: Matematicamente
Titolo o argomento: La rovina del giocatore d’azzardo

Un cammino a caso nel quale un giocatore d’azzardo scommette su degli esperimenti ripetuti, in ciascuno dei quali la sua probabilità di vittoria è strettamente compresa tra 0 e 1. Tale possibilità si conclude quando il giocatore riesce a raddoppiare il suo capitale iniziale oppure quando lo perde completamente.

Ad esempio può iniziare con 5 euro e scommettere sempre 1 fino a che vince 10 euro, oppure perdere tutta la somma iniziale. Tale procedimento dà “le probabilità di transizione di una catena di MARKOV” con due stati assorbenti; la probabilità di andare in rovina dipende sia dallo stato iniziale che dalla probabilità di vittoria di ogni esperimento.

gioco-dazzardo.jpg

Pubblicato il

Cos’è un vettore?

Rubrica: Fisicamente
Titolo o argomento: Che cos’è un vettore

Una qualsiasi grandezza dotata sia di un’intensità che di direzione (e verso) come ad esempio la velocità, l’accelerazione o una forza. Una n-pla  (se non vado errato si legge ennupla) di numeri reali considerata elemento dello SPAZIO EUCLIDEO a n dimensioni. I vettori sono indicati nei diagrammi da frecce che hanno la direzione del vettore stesso e la cui lunghezza è proporzionale all’intensità (o modulo) della grandezza vettoriale rappresentata.

Che cos’è una n-pla? Si tratta di un insieme ordinato di n elementi. Ecco un esempio: Vettore v=[1, 4, 2] ovvero vettore v con x=1, y=4, z=2 che non sono altro che le coordinate per rappresentarlo nello spazio Euclideo (o Cartesiano, è la medesima cosa).

Spazio Euclideo (o Cartesiano): Spazio vettoriale di dimensione finita reale. Lo vedremo più in dettaglio in seguito nei prossimi articoli della nostra rubrica MatematicaMENTE.

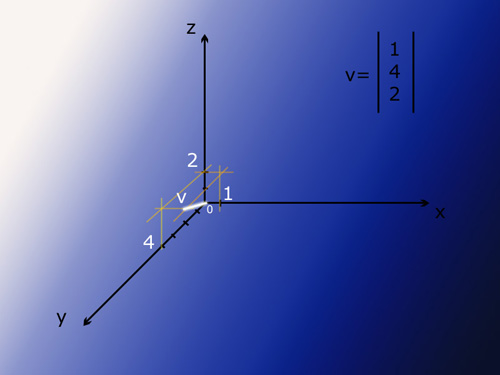
Rappresentazione del vettore V=(1, 4, 2)

Primo esempio

Piacevole, spero, il primo esempio di rappresentazione grafica di vettori. Qui non troverete numeri o formule ma capirete bene il concetto primario essenziale di vettore, cosa rappresenta e a cosa serve in un applicazione vera o simulata.

Simulazione di una corsa automobilistica, i vettori di cui parleremo rappresentano le forze agenti su un veicolo dotato di pneumatici in mescola (quindi con attriti molto elevati). Nella foto è visibile una comune situazione di sovrasterzo per perdita di aderenza al retrotreno:

Vettori 1a in figura. Lo sforzo che agisce sulle ruote anteriori è minimo. Sia longitudinalmente, sia lateralmente. Ciò perchè in questo frangente la vettura ha una perdita di aderenza al posteriore. Quando questa situazione si verifica l’avantreno è poco sollecitato.

Vettori 1p in figura. L’aderenza al retrotreno è bassa, oppure il pilota ha superato il limite sopportato dalla sua vettura e dal suo setup in quella parte di telaio. Forse vi è uno squilibrio nella distribuzione delle masse tra avantreno e retrotreno o forse un problema di aderenza dovuto a campanature eccessive e quindi allo scarso contatto delle gomme a terra o ancora la taratura dei differenziali non permette una buona apertura del gas in quel punto del tracciato ed infine la molle posteriori potrebbero avere una taratura insufficiente e non assorbire le forze che agiscono sul veicolo e che, di conseguenza, sfogano totalmente sulle gomme. Se il setup è corretto, il vettore rosso alle gomme posteriori potrebbe indicarci che il pilota ha effettuato una manovra spettacolare ma che manda in crisi gomme e telaio.

Vettori 2 in figura. Questi vettori indicano la forza che sta agendo su ogni ruota. Ovviamente la ruota sulla quale agisce una maggior forza, andrà in temperatura prima e, probabilmente si usurerà prima.

Vettori 3 in figura. I due vettori chiari al centro del veicolo rappresentano gli effetti giroscopici sul mezzo. Accelerazione longitudinale e accelerazione laterale. Maggiore è l’intensità e quindi la lungezza del vettore che indica l’accelerazione laterale, e maggiore sarà la tenuta di strada.

Vettori 4 in figura. I vettori perpendicolari azzurrini indicano la ripartizione del carico aerodinamico alla determinata velocità di quell’istante. Un vettore troppo intenso al posteriore, ovviamente indicherebbe un eccessivo carico al posteriore, con il risultato che ne consegue di una vettura sottosterzante e viceversa…

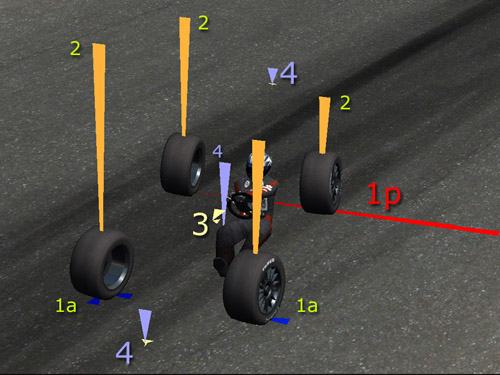
Legenda: il blu rappresenta sforzi minimi, il giallo sforzi nella norma
il rosso sforzi eccessivi e, automaticamente errori di guida o di setup.

Secondo esempio

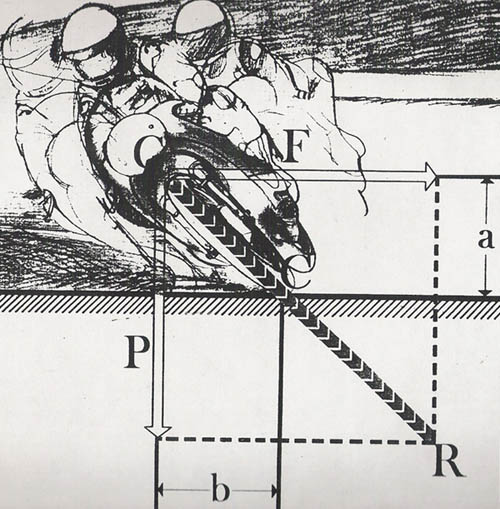
Su due ruote questa volta, lo schema evidenzia grazie ai vettori, la forza peso che spinge la moto verso il basso e la forza che la spinge la moto stessa all’esterno della curva (ovviamente i pneumatici si opporranno dando luogo ad una reazione vincolare uguale e contraria). E’ inoltre visibile il vettore a generato dalla composizione delle 2 forze: il vettore risultante. L’origine dei vettori è nel baricentro dell’insieme moto-pilota.

Approfondimenti

Proviamo a complicare leggermente le cose…

Modulo (o norma) ρ del vettore v

Se v=(x,y) appartenente ad R2 è un vettore non nullo applicato nell’origine, il suo modulo o norma (ovvero la sua lunghezza) è il numero positivo: ρ=|v|=√(x2+y2). Attenzione perchè su alcuni testi trovate il modulo ed il valore assoluto espressi con il medesimo simbolo, mentre su altri testi trovate il valore assoluto espresso come segue |x| ed il modulo (o norma) espresso con la doppia barretta ||v||.

Argomento θ del vettore v

Si tratta di quell’angolo θ appartenente a [0, 2π) che viene misurato in radianti e per il quale x = ρcosθ e y = ρsinθ (vedi l’articolo: “Coordinate polari“).

Link correlati

Forza centrifuga e Forza centripeta
Sistemi di riferimento inerziali
Sistema di riferimento non inerziale

Pubblicato il

Randomizzare

Rubrica: Matematicamente
Titolo o argomento: Cosa significa randomizzare

Scegliere o ordinare i dati, gli individui, ecc. in modo deliberatamente casuale, di solito allo scopo di aumentare l’affidabilità dei risultati statistici ottenuti.

In particolare, significa che la conoscenza dei numeri generati da questo processo, o da un qualunque altro processo, non porta informazioni aggiuntive al riguardo del prossimo numero generato.

Note: ricordo perfettamente, quando frequentavo le scuole superiori all’ITIS, che il mitico professor Raniero Romagnoli sceglieva gli interrogati con la funzionalità RANDOM della sua calcolatrice… Il risultato interessante è che dalla sua calcolatrice su 10 numeri estratti, 8 corrispondevano al numero 2 ovvero Anselmi (il secondo in ordine alfabetico) 🙂

Pubblicato il

Andare in Loop

Rubrica: Matematicamente
Titolo o argomento: Ripetere continuamente

Andare in loop significa ripetere un programma iterativo senza interrompersi.

  • In musica ad esempio si riferisce alla ripetizione continua di un effetto audio campionato.

  • In informatica il loop è una sequenza di comandi che viene ripetuta diverse volte, ma è scritta una volta sola.

  • In matematica il loop è un insime contenente degli elementi (per tanto non è un insieme vuoto) che sono dotati di un’operazione binaria (•): L × L → L

 tale che:

esiste un elemento 1L, detto neutro, tale che

per ogni

l’equazione

ha un’unica soluzione

l’equazione

ha un’unica soluzione

NOTE: per i meno pratici ma comunque desiderosi di capire come si legge la scritta:

(•): L × L → L

(•) il segno tra parentesi è semplicemente il simbolo che viene dato a tale operazione

L è il nome dell’insieme (ovvero un contenitore per elementi matematici)

L × L significa che l’operazione citata viene eseguita all’interno dell’insieme L e con elementi dell’insieme L. Un prodotto cartesiano di L con se stesso.

→ L significa che il risultato di questa operazione matimatica è nuovamente contenuto nell’insieme L. Questo deve essere sottolineato perchè ci sono casi in cui un’operazione eseguita all’interno di un insieme, porta in un altro insieme con altre caratteristiche.

Se qualcuno dei lettori fosse in grado di spiegare meglio il loop in termini di matematica, può scrivere un gradito commento chiarificatore.

Pubblicato il

Il paradosso di Zenone

Rubrica: Matematicamente

Titolo o argomento: Il paradosso di “Achille e la tartaruga”

Il paradosso di Zenone, conosciuto anche come il paradosso di Achille e la tartaruga, attraverso una dimostrazione che trovate facilmente su testi di analisi matematica come sul web, afferma che se Achille (detto pié veloce) darà un piede di vantaggio alla tartaruga, nella loro gara, potrebbero entrambi correre all’infinito tanto Achille non raggiungerebbe mai la tartaruga. Questo perchè Achille per raggiungere la tartaruga dovrebbe raggiungere il punto di partenza poco più avanti della tartaruga e, a questo punto, la tartaruga, avrebbe già compiuto un altro tratto di strada. Achille sarebbe quindi costretto a percorrere pure il nuovo tratto di strada ma, nel frattempo, la tartaruga ne avrebbe compiuto ancora un altro. Risultato del paradosso è quindi che Achille non raggiungerà mai la tartaruga (questa teoria non ha valore fisico ma è stata molto utile nella storia del pensiero filosofico e matematico). Ora a questo punto vorrei fare delle semplici osservazioni a modo mio per sbloccarvi la mente da questo incastro…

Nel primo riquadro osserviamo che Achille e la tartaruga partono dallo stesso punto e Achille raggiunge il traguardo prima della tartaruga ma non solo: percorre anche il doppio dello spazio nello stesso intervallo di tempo. Questo perchè la sua velocità è doppia ( pié veloce).

https://www.ralph-dte.eu/gallery/scienze/matematicamente/achille/osservazione1.swf

Nel secondo riquadro osserviamo che Achille da un vantaggio di un’unità alla tartaruga. Achille arriva ancora primo al traguardo ma non percorre più il doppio dello spazio nello stesso intervallo di tempo, pur essendo rimaste invariate le velocità di entrambi, proprio a causa del vantaggio concesso. Vince comunque Achille.

https://www.ralph-dte.eu/gallery/scienze/matematicamente/achille/osservazione2.swf

Allora quale dovrebbe essere la condizione affinché Achille non raggiunga mai la tartaruga? Colpo di scena: Achille dovrebbe essere anch’egli una tartaruga. A parità di condizioni per così dire prestazionali, avendo quindi lo stesso corpo, le stesse capacità, le stesse caratteristiche, la stessa velocità, la stessa massa e accelerazione e dando il vantaggio anche di un solo piede, Achille non raggiungerebbe mai la tartaruga proprio per la logica espressa dal paradosso di Zenone e cioè perchè dovrebbe prima percorrere il tratto di vantaggio. Un particolare esercizio di riscaldamento per la mente (naturalmente per coloro a cui piacciono queste osservazioni e giocare con la logica). Ecco finalmente Achille, tramutatosi in tartaruga, non raggiungere mai l’avversaria:

https://www.ralph-dte.eu/gallery/scienze/matematicamente/achille/osservazione3.swf

Pubblicato il

Problema di Montmart dell’abbinamento

Rubrica: Matematicamente
Titolo o argomento: Problema di Montmart dell’abbinamento

Il problema di determinare la probabilità che, in un abbinamento casuale di due insiemi accoppiati naturalmente (come due mazzi di carte o un gruppo di lettere e di buste con gli indirizzi) esista almeno un abbinamento corretto.

Tale probabilità tende a: [1-(1/e)] al crescere del numero degli elementi dell’insieme.

La lettera “e” nella formuletta rappresenta per l’appunto  il numero degli elementi dell’insieme.

1-1sux.png