MatematicaMENTE FisicaMENTE LogicaMENTE

15 dicembre 2009

Perchè mi fanno studiare la matematica?

Rubrica: Matematicamente
Titolo o argomento: A cosa serve studiare la matematica?
Ecco quanto spesso gli studenti affermano alle scuole medie inferiori e superiori:

Non mi serve! Quando andrò a lavorare mica mi faranno risolvere equazioni e integrali! A che servono tutti questi calcoli? Non dobbiamo fare tutti lo scienziato! Non farò mai il professore di Matematica. Stiamo perdendo tempo! La Prof. si dilunga su cose inutili. Ecc. Ecc.

Ma tutto questo è vero? Ovviamente no. Ecco un esempio breve, semplice e comprensibile a chiunque:

Se fai l’atleta, ti piace correre e sei un centometrista, sai bene come l’allenamento del tuo corpo sia fondamentale per una buona prestazione e, cosa altrettanto importante, per non farti male. Così vai in palestra, alleni busto braccia e gambe… Quando poi ti schieri ai blocchi di partenza non devi metterti a sollevare pesi. “Devi correre… Più forte che puoi e con la migliore tecnica che hai imparato!”

Quando studi matematica fai la medesima cosa. Molto probabilmente a lavoro, è vero, non dovrai risolvere equazioni o integrali… tuttavia ti sarà richiesto di “ragionare”, di essere logico, avere una mente pronta, allenata, essere sveglio, attivo… La matematica che studi a scuola è fondamentale per “Allenare la tua mente a qualcosa di più grande”.

Non avete nemmeno idea di quante cose riesco a fare da quando ho deciso di studiare la matematica anche al di fuori degli studi scolastici e universitari… Certo è che un fattore penalizzante può essere senz’altro la sfortuna di trovare libri di testo poco chiari, confusionari, troppo densi e con pochi esempi. In quel caso, nemmeno con tutta la passione possibile immaginabile è possibile studiare e capire qualcosa.

2 dicembre 2009

Caos deterministico

Rubrica: Matematicamente

Titolo o argomento: Che cos’è il caos deterministico?

Una tra le più recenti scoperte della matematica sperimentale è il cosiddetto “caos deterministico”.

Quando un sistema dinamico (di qualsiasi natura e scala) è sufficientemente complesso e dotato di interazioni non lineari, la sua evoluzione nel tempo, nonostante sia governata da leggi rigorosamente “deterministiche”, può diventare “caotica”.

La soluzione degli algoritmi che descrivono l’evoluzione di un sistema dinamico prende il nome di “attrattore”. Il nome deriva dal fatto che la soluzione numerica dei sistemi di equazioni è normalmente di tipo iterativo, a “convergenza”. Tutto avviene in sostanza come se essa fosse dotata di un potere di “attrazione”, che appunto la attrae verso la convergenza.

Quando la curva rappresentativa dell’attrattore è “regolare”(un punto, un segmento, un cerchio, un ellisse, una qualsiasi curva unica o periodicamente ripetitiva) si ha un attrattore “ordinario”.

Quando invece è “irregolare” (una curva infinitamente aggrovigliata, mai ripetitiva) si ha un attrattore “strano, cioè “caotico”. La curva infinitamente aggrovigliata che si ottiene è un “frattale”: una linea infinitamente lunga e mai ripetitiva ma contenuta in un’area o un volume (o un iper-spazio) di dimensioni finite.

Il termine “frattale” deriva dal fatto che simili curve infinitamente aggrovigliate su sé stesse, finiscono per assumere caratteristiche di “quasi” superfici, “quasi” volumi, ecc., assumendo così dimensioni non intere, frazionarie, “frattali” appunto.

La più nota rappresentazione visiva di fenomeni caotici è la famosa “farfalla” di Edwin Lorenz la quale mostra l’evoluzione “caotica” del clima fornita da un modello meteorologico del 1963. L’attrattore di Lorenz esprime il noto concetto di “effetto farfalla” e cioè che in sistemi caotici, piccole differenze nelle condizioni iniziali possono originare, dopo un tempo sufficiente, grandi differenze nelle condizioni finali.

Il caos deterministico è stato perciò impropriamente anche definito come la possibilità che “piccole cause possano generare grandi effetti”. In questo senso è diventato famoso l’aforisma di Lorenz secondo cui: ” il battito delle ali di una farfalla in Brasile, può provocare un uragano nel Texas”. In realtà in senso “fisico” è errato dire che “piccole cause possono generare grandi effetti”. E’ invece corretto affermare che un’infinità di microcause (ognuna di per sé trascurabile), agendo su tempi sufficientemente lunghi, possono produrre per accumulo macro effetti non trascurabili.

30 ottobre 200922 ottobre 2018

Il Setup di un’auto di formula

Rubrica: Curiosità tecnica da corsa
Titolo o argomento: Quante combinazioni sono possibili in un setup di un’auto di formula?

Considerando le 24 regolazioni possibili, ossia:

Ride Height (o altezza vettura).
Caster (o incidenza).
Camber (o campanatura).
Toe (o convergenza).
Springs – Le molle.
Damper low speed bump – La compressione dell’ammortizzatore a bassa velocità.*
Damper high speed bump – La compressione dell’ammortizzatore ad alta velocità.*
Damper low speed rebound – L’estensione dell’ammortizzatore a bassa velocità.*
Damper high speed rebound – L’estensione dell’ammortizzatore ad alta velocità.*
Damper piston – Il pistone dell’ammortizzatore.
Damper pression – La pressione nell’ammortizzatore.
Damper bump shimming – Pacchi lamellari che regolano il passaggio dell’olio in compressione.
Damper needle.
Damper rebound shimming – Pacchi lamellari che regolano il passaggio dell’olio in estensione.
Roll center – Centro di rollio.
Antidive – Antilift – Antisquat.
Wings Setting – Angolo delle ali.
Gurney Flaps (o smorzatore di turbolenze sul profilo alare**).
Tires pressure – Pressione pneumatici.
Antiroll bar – Barre anti rollio.
Antiroll bar blades – I bracci che vanno dall’ammortizzatore alla barra antirollio.
Antiroll bar blades position – La posizione dei bracci che vanno dall’ammortizzatore alla barra antirollio.
Bump rubber – Tamponi di fine corsa degli ammortizzatori.
Brake master cylinders – Il dimensionamento dei cilindri dell’impianto idraulico del sistema frenante.

Secondo la matematica con 24 parametri ci sono la bellezza di oltre 79 trilioni di possibilità, il numero esatto è: 79.766.443.076.872,5 di possibilità 😀 Per fortuna la maggior parte di queste possibilità non sono funzionali, pertanto ci si muove all’interno di un range molto ristretto dove il giusto setting è comunque molto difficile da trovare.

VIDEO IN REVISIONE

*Si intende alta o bassa velocità dello stelo dell’ammortizzatore. Quindi un urto (se così vogliamo chiamarlo) più o meno violento. Quando il pilota centra un cordolo, ad esempio, la velocità con cui la ruota spinge e quindi comprime l’ammortizzatore è molto maggiore di quando gradualmente entra in curva ed il mezzo si corica verso l’esterno.

**E’ la traduzione italiana che ho dato io dato che non ce n’é una ufficiale 🙂

3 agosto 2009

Che cos’è un algoritmo?

Rubrica: Matematicamente
Titolo o argomento: Che cos’è un algoritmo

Si tratta di una procedura a passi tramite la quale è possibile compiere un’operazione senza utilizzare l’intelligenza e quindi tramite una macchina. Formalmente è la descrizione ricorsiva di una procedura tramite la quale un determinato tipo di problema può essere risolto grazie ad un numero finito di passaggi meccanici. Nell’estrazione di radice e nelle divisioni lunghe sono utilizzati algoritmi familiari dell’aritmetica elementare.

La teoria della COMPUTIBILITA’ studia quanta parte della matematica può essere descritta in tali termini e il PROGRAMMA di HILBERT era fondamentalmente un tentativo di dimostrare che tutta la matematica è derivabile da algoritmi che operano su stringhe di simboli matematici.

17 giugno 2009

Sistema di riferimento non inerziale

Rubrica: Fisicamente
Titolo o argomento: Sistema di riferimento non inerziale

Segue dal precedente articolo: Sistema di riferimento inerziale.

I sistemi inerziali sono i sistemi rispetto ai quali le leggi del moto assumono la forma più semplice (se hai a disposizione un testo di Fisica Generale, vedi anche: principio di relatività, i tre principi di Newton, momento di una forza e momento della quantità di moto).

Un sistema di riferimento in moto rettilineo uniforme rispetto ad un riferimento inerizale è anch’esso inerziale e le leggi della dinamica trovano conferma sperimentale con lo stesso grado di esattezza tanto nel primo quanto nel secondo. Così un treno ideale che corre a velocità costante senza scosse su binari diritti ed orizzontali costituisce un sistema inerziale negli stessi limiti in cui lo è la terra; una valigia appoggiata sul portabagagli è in equilibrio e vi rimane ferma (vale il principio di inerzia).

Ma se il treno si arresta bruscamente o accelera bruscamente, diventando così un sistema accelerato rispetto alla Terra e dunque non inerziale, si producono dei fatti insoliti non prevedibili con le leggi di Newton: la valigia, per esempio cade dalla rete del portabagagli. Da un punto di vista fisico vuol dire semplicemente che le leggi della dinamica non possono più applicarsi se il sistema di riferimento non è inerziale e tutto avviene come se sui corpi agissero forze che dipendono dall’accelerazione del sistema di riferimento ma non derivano dalle interazioni con gli altri corpi. Per questo motivo tali forze sono dette apparenti o fittizie.

Proseguiremo questa breve rubrica con la risposta alla domanda del nostro lettore circa quello che rileva un accelerometro quando un’auto (stradale o da corsa che sia) percorre una curva.

Continua…

17 giugno 2009

Sistema di riferimento inerziale

Rubrica: Fisicamente
Titolo o argomento: Sistema di riferimento inerziale

Sistema costituito da corpi NON soggetti ad interazioni.

Sappiamo che il moto è relativo, nel senso che i vettori posizione, velocità ed accelerazione di una particella dipendono (in modulo, direzione, verso) dal sistema al quale viene riferito il moto della particella.

In generale prima di arrivare alla formulazione di qualche legge è necessario precisare il sistema di riferimento rispetto al quale intendiamo descrivere il moto della particella.

Intanto ricordiamo che un sistema fisico di riferimento è costituito da un insieme di oggetti, arbitrariamente scelti, collegati ad una terna di assi cartesiani.

Gli oggetti che costituiscono, per così dire, il sostegno del sistema di riferimento possono interagire con i corpi che li circondano. E per conseguenza questi oggetti possono muoversi l’uno rispetto agli altri, facendo variare così le loro reciproche distanze e rendendo perciò impossibile la determinazione delle coordinate delle particelle osservate.

E’ necessario allora scegliere un sistema di riferimento che sia soggetto il meno possibile agli effetti dell’interazione con altri corpi. Sappiamo infatti che le interazioni che ci sono note fra due corpi diminuiscono piuttosto rapidamente al crescere della distanza fra loro. Sicchè ragionevolmente si può suporre che oggetti molto lontani fra loro e da tutti gli altri che li circondano, praticamente non subiscono influenze per effetto di interazioni.

Se si pensa che una stella dista da un’altra almeno diecimilia miliardi di km, ci sentiamo sufficientemente autorizzati a ritenere che un gruppo di quattro stelle, opportunamente scelte, e collegate ad una terna di assi cartesiani, possa costituire un sistema fisico di riferimento libero, cioè non soggetto ad interazioni.

Un tale sistema si chiama sistema di riferimento inerziale. In generale un sistema di riferimento inerziale è un sistema costituito da corpi non soggetti ad interazioni (almeno entro i limiti degli errori sperimentali).

Da questo punto di vista un sistema collegato alla Terra non è inerziale, perchè la Terra interagisce gravitazionalmente con il Sole e, più debolmente, con gli altri pianeti. Tuttavia un tale sistema può essere considerato con buona approssimazione inerziale quando l’osservazione viene protratta per un intervallo di tempo talmente breve, da poter ritenere la velocità della Terra costante (come se fosse nulla l’interazione con il Sole) e trascurabile l’angolo con cui essa ruota intorno al proprio asse (1 grado ogni 4 minuti).

I sistemi inerziali sono i sistemi rispetto ai quali le leggi del moto assumono la forma più semplice (se hai a disposizione un testo di Fisica Generale, vedi anche: principio di relatività, i tre principi di Newton, momento di una forza e momento della quantità di moto).

Continua…

Continua con: Sistema di riferimento non inerziale.

Perchè la necessità di questo articolo?

A breve risponderemo ad un lettore che ci chiede informazioni su cosa visualizza un accelerometro quando una vettura da corsa percorre una curva dopo un lungo rettilineo. Ci sembrava logico fare prima opportune anticipazioni di Fisica per rispondere correttamente al suo quesito.

Continua…

20 maggio 2009

Esempio di studio di funzione con 2 moduli

Rubrica: Matematicamente, Speciale funzioni matematiche – 5
Titolo o argomento: Esercizio svolto in modo chiaro in ogni sua parte

Ecco a voi passaggi semplici e con tutte le spiegazioni passo passo che spesso ci imbarazziamo a chiedere ai professori. La funzione che andiamo a studiare presenta più particolarità e dettagli del normale, ragione per cui è stata scelta.

Clicca qui per vedere lo studio della funzione

!! pdf in aggiornamento !!

Spiegato ed illustrato passo dopo passo. Tratto da un appello di Analisi Matematica 1

Un esercizio piuttosto articolato che richiede di “ragionare”, motivo per cui ve lo spieghiamo con calma. Non impiegherai più di due ore nel leggerlo e rileggerlo più volte… Uno sforzo che vale la pena fare per prepararsi ad un simile esame con una grande quantità di esercizi.

Suggerimenti:

Dai una scorsa veloce all’intera pagina allegata
Successivamente inizia a leggere ogni argomento con calma senza avere fretta di finire subito
Rileggi la stessa cosa più volte fino a capire i motivi di ogni passaggio
Verifica i conti su un foglio
Ripassa le disequazioni di primo e secondo grado e quelle fratte
Confronta il grafico presente sulla pagina con quello che otterrai ad esempio dalla calcolatrice scientifica
Procurati una tabella delle derivate
Leggi i precedenti articoli di Matematicamente speciale funzioni matematiche…

… Li trovi selezionando MatematicaMENTE nelle categorie a lato di questo BLOG.

Link correlati

Speciale funzioni matematiche -1- Introduzione al concetto di funzione
Speciale funzioni matematiche -2- Dom Codom Invertibilità Monotonia
Speciale funzioni matematiche -3- Elenco funzioni matematiche note
Speciale funzioni matematiche -4- Come si studia una funzione
Speciale funzioni matematiche -5- Esercizio svolto in ogni sua parte

29 aprile 2009

Come si studia una funzione matematica

Rubrica: Matematicamente, Speciale funzioni matematiche – 4

Titolo o argomento: Come si studia una funzione matematica
Le principali cose da osservare

Innanzi tutto ti anticipiamo che più sembra complicata la funzione e più ques’ultima si semplifica, tuttavia negli appelli di Analisi Matematica 1 esistono funzioni senz’altro più lunghe da studiare ma non per questo particolarmente difficili. E’ necessario distinguere la difficoltà dalla lunghezza dello studio di una funzione. Vedremo nei prossimi articoli interessanti esercizi svolti e spiegati in modo realmente elementare. Se ci seguite già da ora vi consigliamo di ripassare le equazioni e le disequazioni di 2° grado, nonché derivate e calcolo dei limiti, prima di attingere agli esercizi svolti che pubblicheremo. Un minimo impegno da parte vostra è logicamente indispensabile 😀

Potrebbe interessarti leggere l’articolo: “Analisi Matematica 1: Metodo di studio e divisione del lavoro”

I passaggi fondamentali e, soprattutto, i perchè

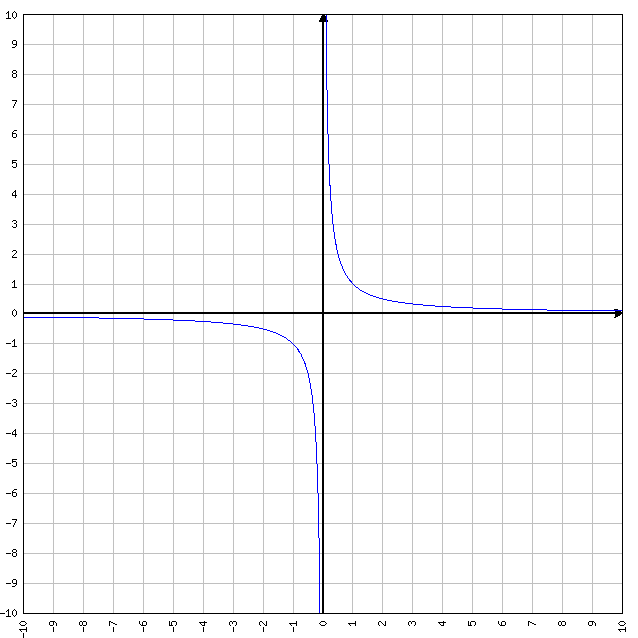
DOMINIO o insieme di definizione della Funzione. Ci serve, in parole povere, per sapere dove, sugli assi cartesiani, la funzione sarà presente o meno (dove potrà passare il grafico e dove no). Solitamente indichiamo con un tratteggio il punto o uno dei punti dell’asse X dove la funzione NON ESISTE. E’ probabile che in questi particolari punti ci siano degli asintoti come vedremo più avanti. Nell’esempio in figura sotto: Y=X/(X-2), il dominio è D=R-[2]. Questo perchè, ovviamente Y= 2/0 NON ESISTE. Viceversa se la funzione fosse stata il reciproco y=(x-2)/2, essendo y=0/2, allora la funzione sarebbe ESISTITA e sarebbe valsa ZERO. Il relativo dominio sarebbe stato tutto R (ovvero tutto l’insieme dei numeri Reali).

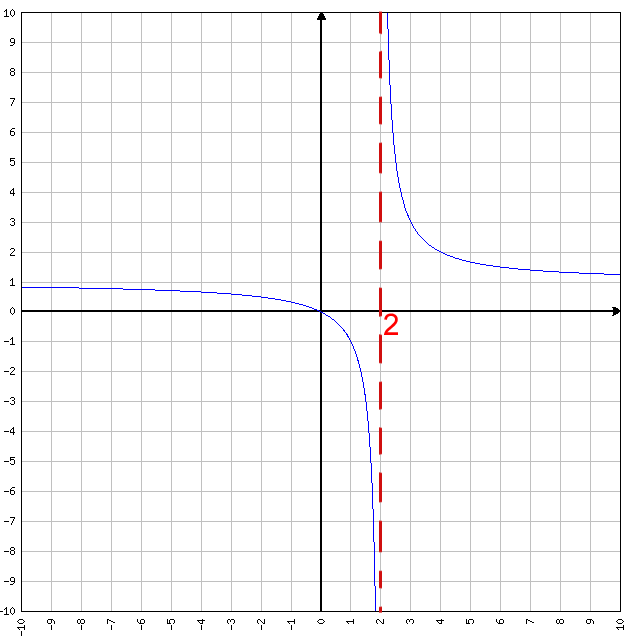
y=x/(x-2)

Si analizza se la funzione che andiamo a studiare ha qualche SIMMETRIA ovvero se è PARI o DISPARI…

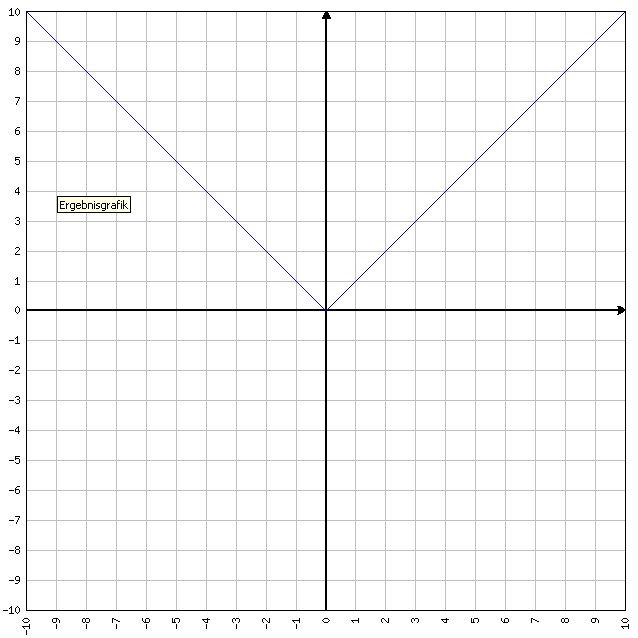
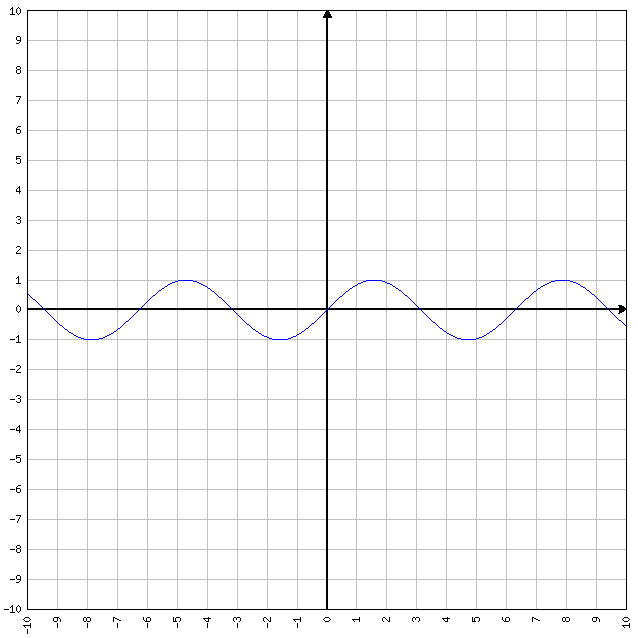
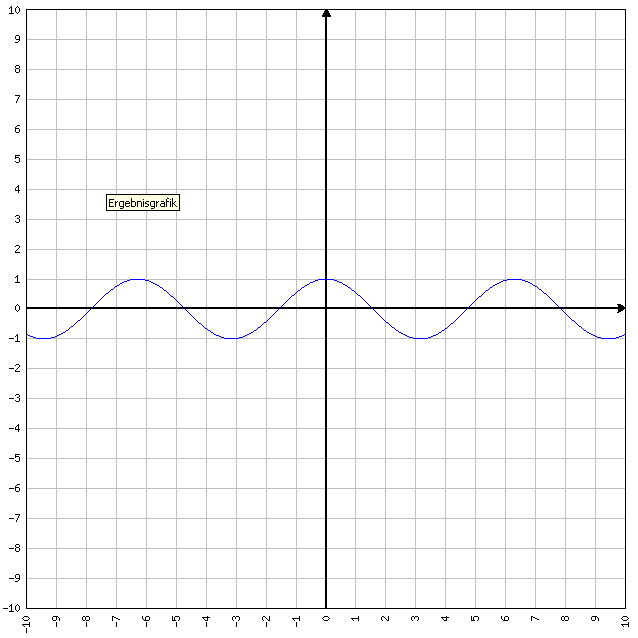
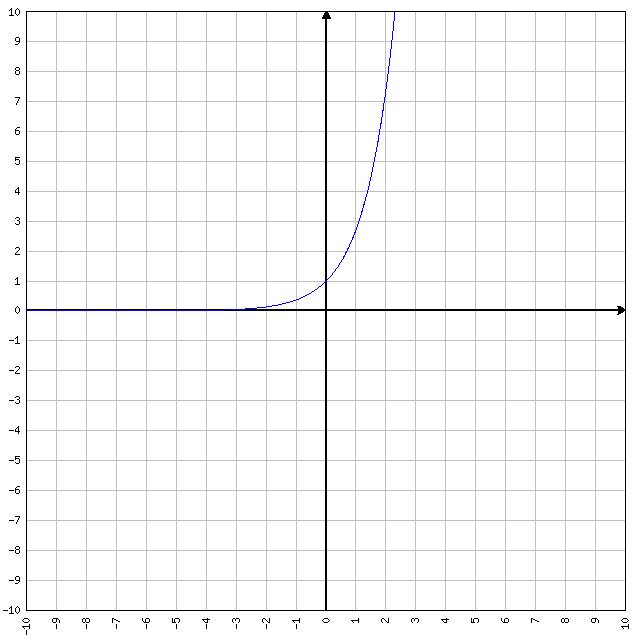
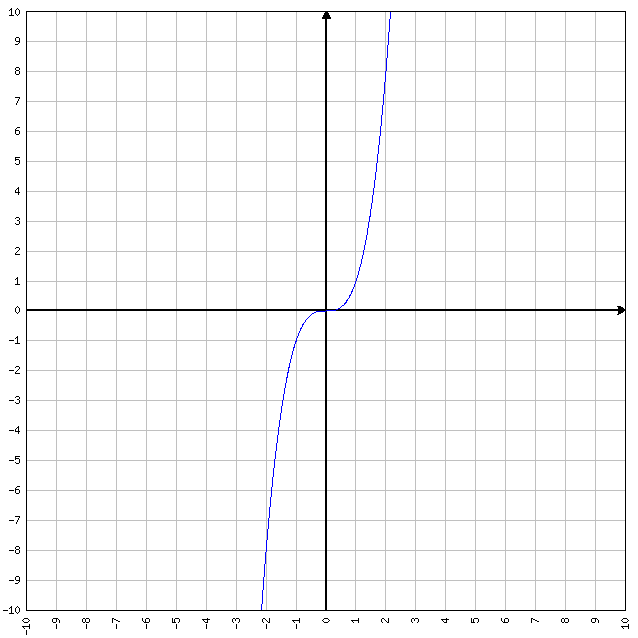
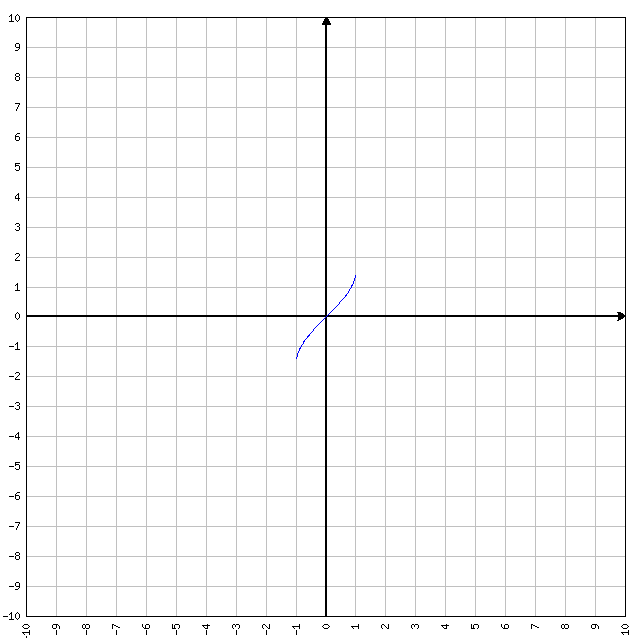
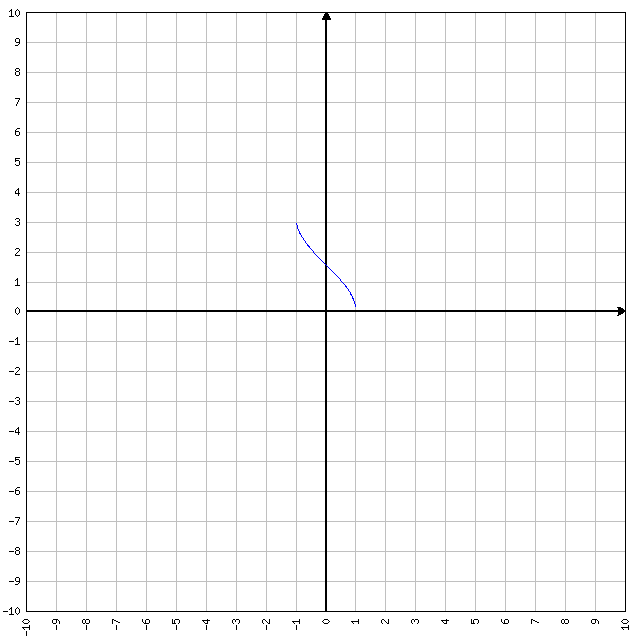
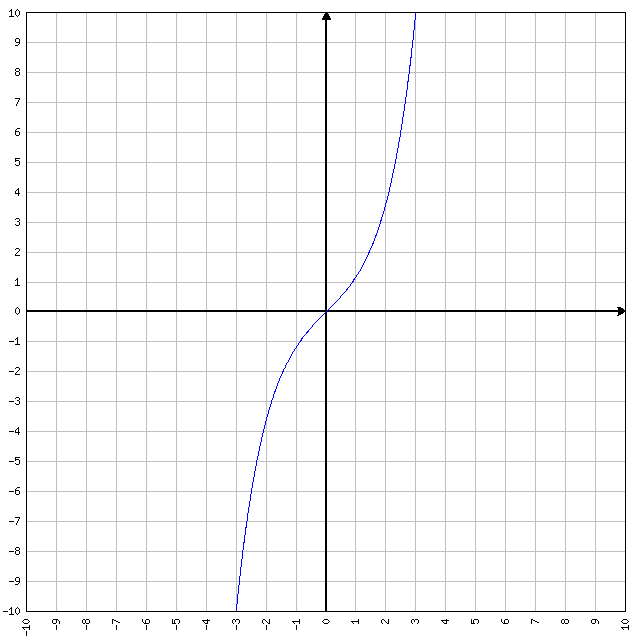
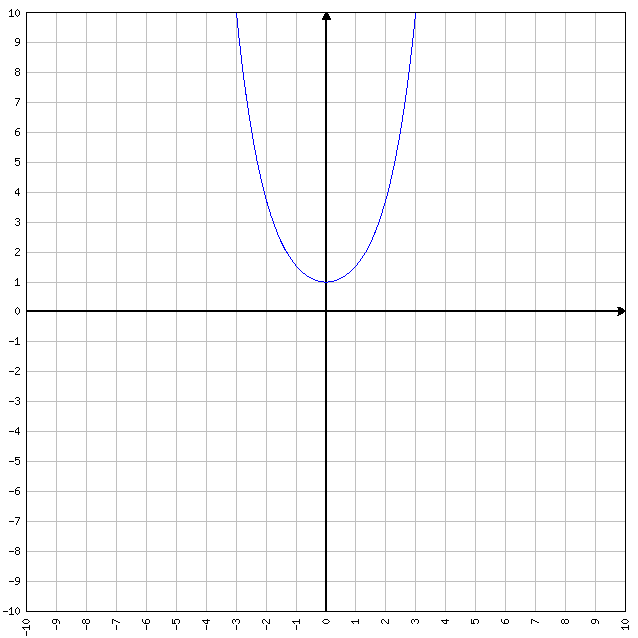
FUNZIONE PARI: se f(-x)=f(x) allora la funzione è pari in quanto sostituendo (AD ESEMPIO) alla x sia il valore 2 , sia il valore -2, otteniamo lo stesso “output”. Tipiche funzioni pari sono y=x^2 (che significa X elevato alla seconda) e y=cos(x). Se ad y=x^2 sostituiamo x=-2 oppure x=2, la funzione da sempre come valore d’uscita y=4. Quindi è pari.

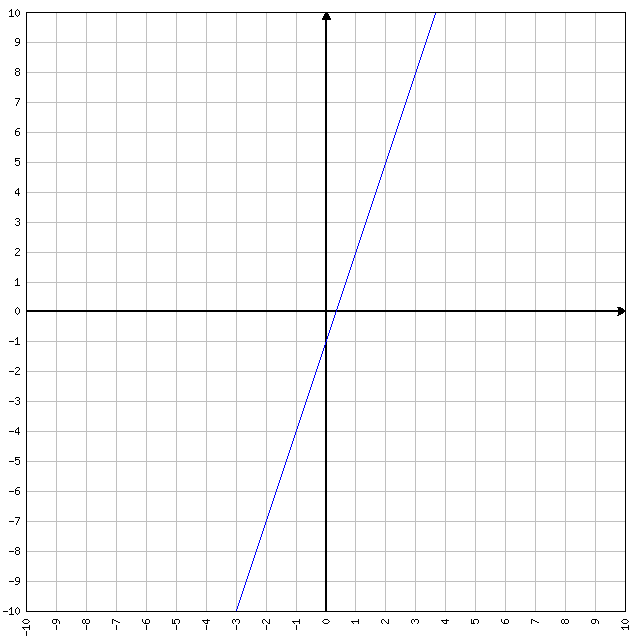
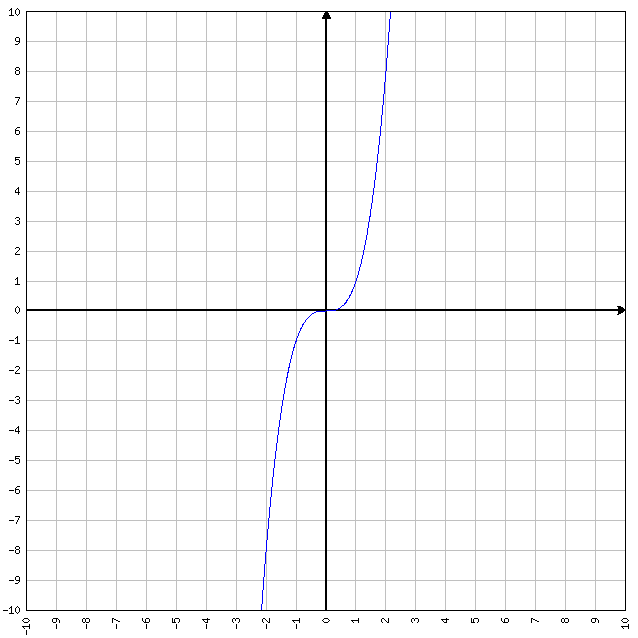
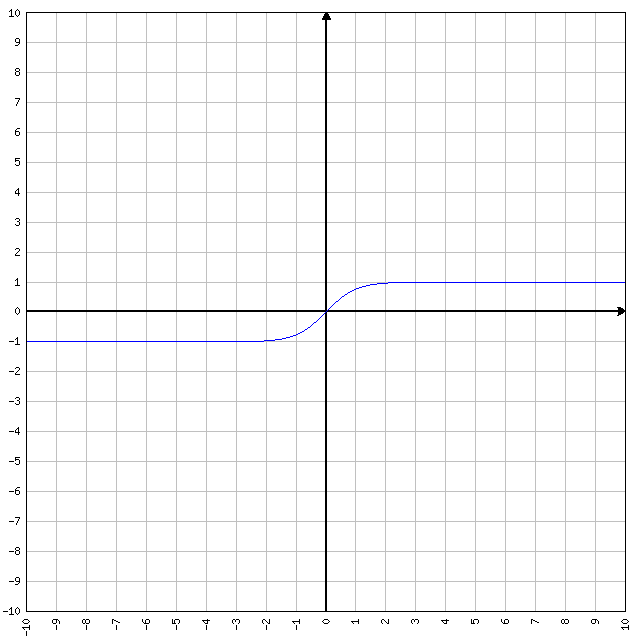
FUNZIONI DISPARI: se f(-x)=-f(x) allora la funzione è dispari. Tipiche funzioni dispari sono y=x e y=sen(x). Se ad y=x sostituiamo x=-1 oppure x=1, otteniamo differenti valori della y.

ASINTOTO VERTICALE:

lim_x→X0f(x) = ± ∞

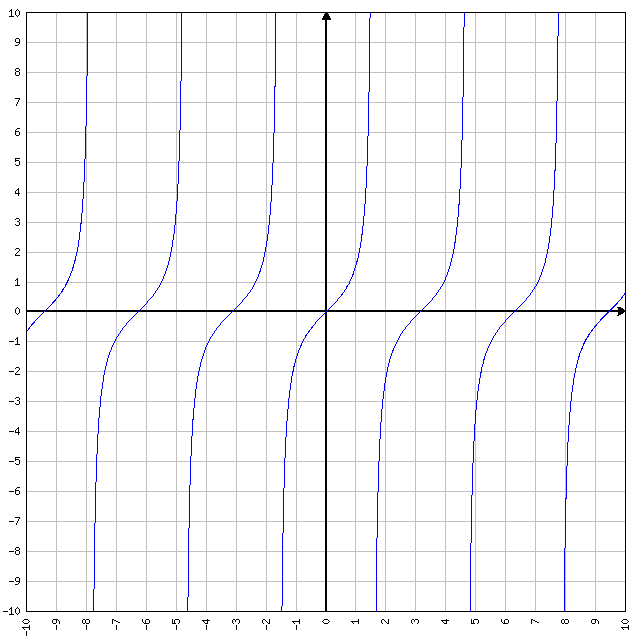
Se sull’asse delle X, più ci avviciniamo ad un punto (X0) e più la funzione va verso +∞ oppure -∞, allora ci troviamo davanti ad un asintoto verticale. Non serve ricordarsi il limite scritto qui sopra a memoria… è più facile ricordarsi l’immagine sotto ed il senso che ha.

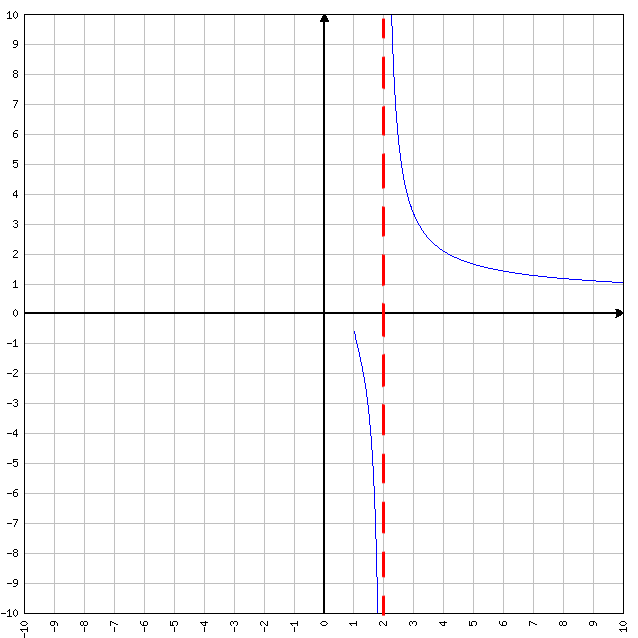
y=1/log(x-1)

ASINTOTO ORIZZONTALE:

lim_x→±∞f(x) = L (appartenente ad R)

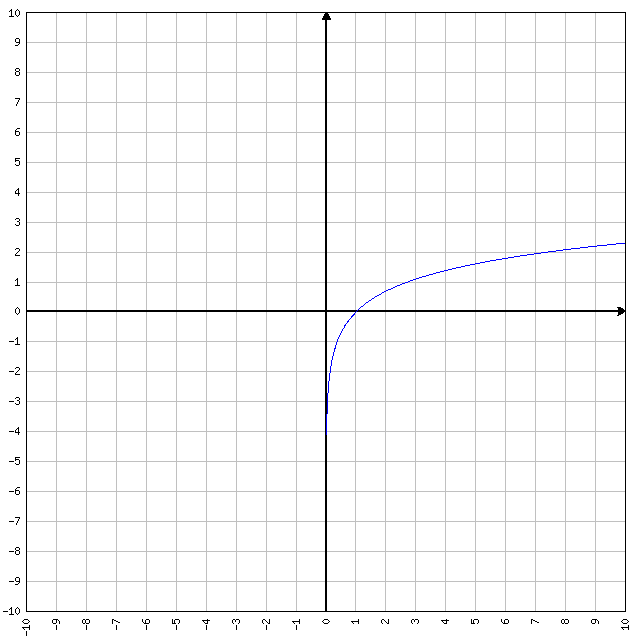
Se sull’asse delle X, più ci spingiamo all’infinito (± infinito) e più la funzione si avvicina asintoticamente ad un punto preciso dell’asse delle y, allora ci troviamo davanti ad un asintoto orizzontale. Non serve ricordarsi il limite scritto qui sopra a memoria… è più facile ricordarsi l’immagine sotto ed il senso che ha. Più andate avanti verso +∞ e più la funzione si avvicina asintoticamente alla retta y=2 (tanto per fare un esempio). In questo particolare esempio questo accade anche muovendosi verso -∞ ma non è detto sia per forza così.

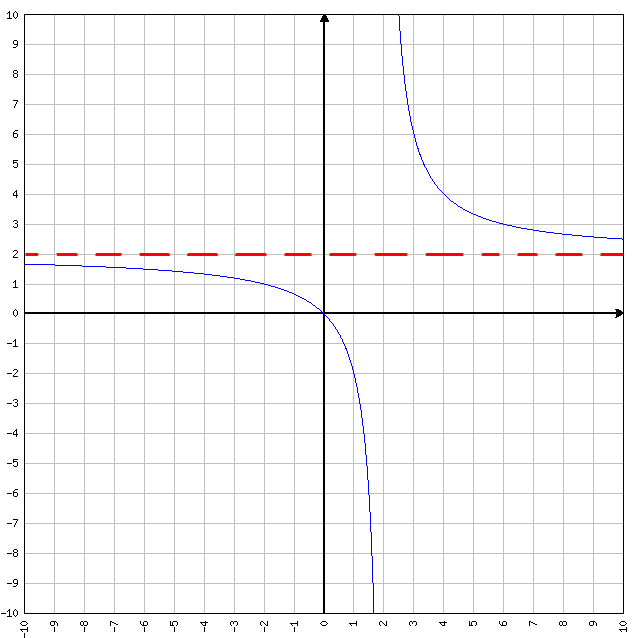
y=(2x)/(x-2)

ASINTOTO OBLIQUO

Anticipiamo subito che se la funzione è dotata di asintoto orizzontale, è inutile andare a cercare l’asintoto obliquo. Calcolandolo trovereste nuovamente l’equazione della retta dell’asintoto orizzontale. Se c’è asintoto orizzontale non c’è asintoto obliquo.

L’equazione dell’asintoto obliquo è l’equazione lineare:

y=mx+q ovvero: y-mx-q=0 → [y-(mx+q)]=0 → [f(x)-(mx+q)]=0

ed il limite dell’asintoto obliquo è: lim_x→+∞[f(x)-(mx+q)]=0

dove:

m=lim_x→+∞f(x)/x

q=lim_x→+∞[f(x)-mx]

E’ ovvio che se c’è asintoto orizzontale (ad esempio y=2) ne segue che m=0 in quanto sarebbe: y= 0·x + q ovvero: y= q (nel nostro esempio y=2). Ragione per cui non ha senso calcolare l’asintoto obliquo se vi è quello orizzontale.

y=(x-1)³/(x-2)² il cui asintoto obliquo vale y=x+1

m=lim_x→+∞[(x-1)³/(x-2)²]/x=1

q=lim_x→+∞[((x-1)³/(x-2)²)-mx]=1

INTERVALLI DI CRESCENZA – DECRESCENZA

Dov’è che il grafico cresce? Dove decresce? In che punto raggiunge un minimo o un massino? Calcola la derivata prima della funzione che stai studiando

Crescenza quando f'(x)>0 Il risultato è l’intervallo nel quale la funzione cresce.

Decrescenza quando f'(x)<0 Il risultato è l’intervallo nel quale la funzione decresce.

Massimo o minimo relativo quando f ‘(x)=0. Quando la “derivata prima” si azzera ci troviamo davanti ad un massimo o minimo relativo.

Intuiamo se si tratta di un massimo o un minimo già osservando i limiti precedentemente studiati, oppure osservando se la funzione cresce e poi decresce (ad esempio) ci troviamo davanti ad un massimo relativo (è ovvio… perchè?) o viceversa… O ancora possiamo capire se ci troviamo davanti ad un massimo o un minimo relativo studiando Convessità – Concavità.

INTERVALLI DI CONVESSITà – CONCAVITà

Dov’è che il grafico è convesso? Dov’è che il grafico è concavo? Cos’è un punto di flesso? Calcola la derivata seconda della funzione che stai studiando

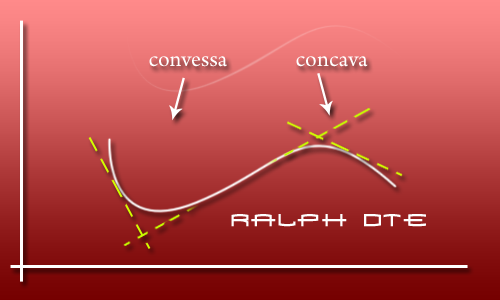
Convessa quando f ”(x)>0 Il risultato è l’intervallo nel quale la funzione è convessa.

(Graficamente) Convessa quando le rette tangenti si trovano sotto la curva.

Concava quando f ”(x)<0 Il risultato è l’intervallo nel quale la funzione è concava.

(Graficamente) Concava quando le rette tangenti si trovano sopra la curva.

Flesso quando f ”(x)=0

Continua…

Link correlati

1 aprile 2009

Funzioni note: seno, coseno, tangente, arcotangente, potenza, esponenziale, logaritmo

Rubrica: Matematicamente, Speciale funzioni matematiche – 3

Titolo o argomento: Funzioni matematiche note (un rapido elenco)

Un elenco apparentemente lungo… …in realtà sintetico, per sapere le generalità in modo veloce

Andando un pò più nello specifico rispetto al precedente articolo sulle funzioni matematiche desidero elencarvi e illustrarvi le più comuni funzioni note. Questo perchè ho notato come durante gli esami orali, studenti che hanno preso ottimi voti allo scritto, non sanno bene come rappresentarle su un foglio e soprattutto non ne conoscono il dominio e il codominio… Fatto strano ma che accade spesso.

Legenda: Indicherò con D il dominio della funzione, con C il codominio e con I l’intervallo di invertibilità della funzione. Mi raccomando, abituatevi al pensiero di cosa vogliano dire i suddetti termini anche perchè ogni testo che trovate adotta diverse lettere per rappresentarli e così ogni sito, forum ecc… Se non imparate a memoria ma ne conoscete il significato non incontrerete problemi insormontabili.

Funzioni lineari

Un esempio semplice y=3x-1 ma potrebbe essere una qualunque altra funzione nella forma y=mx+q. Quando dobbiamo descrivere un asintoto obliquo in uno studio di funzione si ricorre ad una funzione lineare.

Funzione valore assoluto (modulo)

Un esempio y=|x| che è y=x se x≥0 oppure y=-x se x ≤0 esattamente come si vede nell’immagine sopra. In una qualunque funzione contenente il modulo(vedremo in seguito), si vede dove questo si azzera e poi si definisce l’argomento positivo oltre il punto in cui si azzera e negativo prima dello stesso punto. Se vi è più di un modulo, il metodo di risoluzione diventa molto simile a quello delle disequazioni… ma lo vedremo nello specifico in seguito.

y=|x|

Dominio uguale a tutto l’insieme dei Numeri Reali D=R
Codominio contenuto tra zero e più infinito C= [0,+∞)
Invertibilità tra zero e più infinito I=[0,+∞)

Funzione seno

y = sin x

D=R
C=[-1,1]
I=[-π/2, π/2]
potete ricordarvi che il seno di zero vale zero come vedete nell’immagine sopra, per ricordarvi come disegnarla e per non fare confusione con il coseno.

Funzione coseno

y = cos x

D=R
C=[-1,1]
I=[0, π]

Funzione tangente

y = tg x

D=R-[π/2+kπ]
C=R
I=(-π/2, π/2)
Può essere interessante notare che la tangente, essendo uguale al seno fratto il coseno, non esiste quando il coseno vale zero. Ovviamente.

Funzione potenza

y = xⁿ

Nell’immagine sopra a sinistra abbiamo y = x²

D=R
C=[0, +∞)
I= [0, +∞)

Mentre in quella a destra abbiamo y = x³

D=R
C=R
I=R

Funzione esponenziale

y = a^x

D=R
C=(0, +∞)
I=R

Funzione logaritmo

y = log_ax

D=(0, +∞)
C=R
I=(0, +∞)

Funzione arcotangente

y = arctg x

D=R
C=(-π/2, π/2)
I=R
Si tratta della funzione inversa della tangente ossia tan^-1x

Funzione arcoseno

y = arcsen x

D=[-1, 1]
C=[-π/2, π/2]
I=[-1, 1]
Funzione inversa del seno

Funzione arcocoseno

y = coseno x

D=[-1, 1]
C=[0, π]
I=[-1, 1]
Funzione inversa del coseno

Funzione cotangente

Potete provare a ricavare voi i dati sapendo che la tangente è data dal rapporto tra il seno diviso il coseno, mentre la cotangente è il reciproco ossia è data dal rapporto tra il coseno diviso il seno.

Funzione arcocotangente

Potete provare a ricavare voi i dati sapendo che l’arcocotangente è la funzione inversa della cotangente.

Funzioni iperboliche

Seno iperbolico

y = senh x

D=R
C=R
I=R
la sua funzione inversa è la funzione settore seno iperbolico

Coseno iperbolico

y = cosh x

D=R
C=[1, +∞)
I= Non è invertibile su R. Nota però che il coseno iperbolico, come applicazione da [0,+∞) in [1,+∞) è invertibile
la sua funzione inversa è la funzione settore coseno iperbolico