
Rubrica: Officina della Matematica
Titolo o argomento: Prodotto scalare, prodotto vettoriale, prodotto misto
Premessa
Per i neofiti riportiamo di seguito il link all’articolo che definisce in modo semplice ed intuitivo la differenza tra grandezze scalari e grandezze vettoriali: Grandezze scalari – Grandezze vettoriali. Inoltre si precisa che la somma e sottrazione di vettori viene omessa in questo articolo per l’estrema semplicità di tali operazioni.
Prodotto scalare
Si tratta di un prodotto tra vettori (un’operazione binaria) che non mi restituisce un vettore bensì uno scalare. Esso si indica con v·w oppure con (v, w) o, più frequentemente, con <v, w>. Il prodotto scalare di due vettori v e w corrisponde alla norma di v moltiplicata per la norma di w moltiplicata per il coseno dell’angolo compreso tra i due vettori, ovvero: <v, w> = ||v||·||w||·cosθ. Il prodotto scalare è nullo quando almeno uno dei due vettori è nullo oppure quando questi sono ortogonali (infatti cosπ/2=0). In pratica il prodotto scalare tra due vettori è uguale al modulo (o norma) di un vettore per la proiezione dell’altro vettore sul primo.
Assiomi del prodotto scalare
1. Il prodotto scalare è positivo definito: per ogni vettore dello spazio vettoriale V abbiamo <v, v> ≥ 0.
2. Il prodotto scalare è bilineare, v→<v, w> è funzione lineare in v; w→<w, v> è funzione lineare in w.
3. Il prodotto scalare è simmetrico: <v, w> = <w, v>
Relazioni
Prodotto scalare di due vettori v1(x1, y1) e v2(x2, y2): <v, w> = ||v||·||w||·cosθ = (x1·x2)+(y1·y2).
Coseno dell’angolo: cosθ = <v, w>/||v||·||w||, l‘angolo ovviamente lo ricavo dalla funzione inversa del coseno.
Se θ= π/2 allora cosθ=0 e quindi <v, w> = ||v||·||w||·cosθ = 0
Se θ=0 allora cosθ=1 e quindi <v, w> = ||v||·||w||·cosθ = ±||v||·||w||
Additività rispetto alla prima variabile: (v1+v2, w) = <v1, w>+<v2, w>
Omogeneità rispetto alla prima variabile: <λv, w> = λ<v, w>
Lo stesso concetto si ripete per l’additività e l’omogeneità rispetto alla seconda variabile.
Norma di un vettore: ||v|| = √(x2+y2) pertanto ||v|| = √<v, v>
Norma al quadrato di un vettore: ||v||2 = x2+y2
Il prodotto scalare di un vettore per sè stesso è uguale alla norma del vettore al quadrato: <v, v> = ||v||2
Il prodotto scalare della differenza di vettori è uguale alla norma al quadrato della suddetta differenza: <w-v, w-v> = ||w-v||2.
La proiezione ortogonale w di v2 su v1 vale: w = ||v2||·cosθ·(v1/||v1||) = (<v2, v1>/<v1, v1>)·v1.
A cosa serve un prodotto scalare?
Oltre a moltiplicare i moduli di due vettori, permette di calcolare la distanza tra due polinomi, l’angolo tra due applicazioni lineari, la proiezione ortogonale di una matrice…
Prodotto scalare su V
Un prodotto scalare su uno spazio vettoriale è una forma bilineare g simmetrica, questo significa che per ogni coppia di vettori v, w dello spazio vettoriale, il prodotto scalare è l’applicazione g(v, w) = g(w, v) anche se convenzionalmente, come abbiamo indicato all’inizio dell’articolo, detto prodotto viene indicato solitamente con v·w oppure con (v, w) o, prevalentemente, con <v, w>.
Nota che una forma bilineare sullo spazio vettoriale V è un’applicazione secondo la quale:
g(v1+v2, w) = g(v1, w) + g(v2, w)
g(v, w1+w2) = g(v, w1) + g(v, w2)
g(λv, w) = λg(v, w) = g(v, λw)
Nucleo di un prodotto scalare
Il nucleo di un prodotto scalare è costituito dall’insieme dei vettori v che, moltiplicati scalarmente per qualunque generico vettore w, mi restituiscono zero. C’è una certa somiglianza logica con il nucleo di un’applicazione lineare ovvero il KerT (vedi l’articolo: Dimensione – Nucleo Ker – Immagine – Rango). Il nucleo di un prodotto scalare si indica apponendo alla lettera V un apice a forma di T rovesciata.
Prodotto scalare degenere e non degenere
Un prodotto scalare su V si dice degenere se il suo nucleo contiene degli elementi altrimenti, se il suo nucleo è vuoto, si dice non degenere.
Prodotto vettoriale
Si tratta di un prodotto tra due vettori linearmente indipendenti, che determinano quindi un piano, definito unicamente su R3. Il risultato in uscita è ancora una volta un vettore la cui particolarità è l’ortogonalità rispetto ai due vettori moltiplicati. Il prodotto vettoriale tra i vettori v e w si indica con ^ e quindi ad esempio v^w (in realtà il simbolo corretto è una v minuscola rovesciata), in alternativa si può utilizzare il simbolo della moltiplicazione imparato alle elementari che assomiglia ad una x, ovvero ×, quindi ad esempio v×w. Il prodotto vettoriale di due vettori v e w corrisponde alla norma di v moltiplicata per la norma di w moltiplicata per il seno dell’angolo compreso tra i due vettori, ovvero: v×w = ||v||·||w||·senθ. Il prodotto vettoriale è nullo quando uno dei due vettori è nullo oppure i due vettori moltiplicati sono linearmente dipendenti (collineari o paralleli) e quindi l’angolo compreso tra i due è zero ed il relativo seno vale a sua volta zero (infatti sen0=0). In pratica il prodotto vettoriale è uguale ad un terzo vettore ortogonale ai due moltiplicati.
Assiomi
1. Il prodotto vettoriale è lineare in ciascuno dei due fattori ovvero è bilineare
2. Il prodotto vettoriale è ortogonale a entrambi i fattori: (v×w)⊥v; (v×w)⊥w
3. La norma di v×w è l’area del parallelogramma (di vertici o, v, w, v+w) generato da v e w: ||v×w||=Area
4. v×w=0 se e solo se v e w sono linearmente dipendenti
5. Se v e w sono line. indip. allora la base (v, w, v×w) determina la stessa orientazione della base canonica
6. v×w è l’unico vettore che soddisfa i punti 2, 3, 5
7. Il prodotto vettoriale è anticommutativo: w×v = -v×w
8. Il prodotto vettoriale è distributivo: v×(w1+w2) = v×w1 + v×w2
9. Il prodotto vettoriale non è associativo
Relazioni
Se abbiamo i vettori v=(vx, vy, vz) e w=(wx, wy, wz) allora il prodotto vettoriale dei due equivale al determinante della matrice seguente:

A cosa serve un prodotto vettoriale?
Può essere utilizzato per esprimere la distanza di un punto da una retta, la distanza tra due rette, l’area del parallelogramma generato dai due vettori moltiplicati…
Prodotto misto
Dati tre vettori u, v, w il loro prodotto misto è una quantità scalare che individua il volume del parallelepipedo da essi generato preso con il segno positivo o negativo a seconda che la terna u, v, w sia destra o sinistra (vedi la regola della mano destra), questo vale: u × v · w = (u × v) · w
Relazioni
Volume parallelepipedo: <(u×v), w> = (v·w·senα)·(w·cosβ) = area base parallelepipedo · altezza parallelepipedo
Se abbiamo i vettori u=(ux, uy, uz), v=(vx, vy, vz) e w=(wx, wy, wz) allora il prodotto misto dei tre equivale al determinante della matrice seguente:
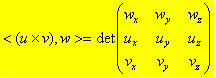
Doppio prodotto vettoriale
Descrizione in preparazione
Divisione vettoriale
Descrizione in preparazione

