Rubrica: Officina della Matematica
Titolo o argomento: La logica della composizione di funzioni
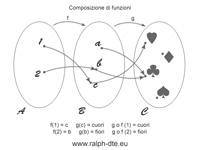
Composizione di funzioni
Il concetto di composizione di funzioni viene definito come una relazione tra due funzioni “f:A→B” e “g:B→C” ove il codominio di f coincide con il dominio di g. Ciò permette di definire una nuova funzione che corrisponde alla composizione di f con g, che si scrive “g o f” e si legge “g composto f” (nel caso specifico si scrive “g o f: A→C”).
Composizione di applicazioni lineari
Il concetto è assolutamente il medesimo: una relazione tra due applicazioni lineari “S:U→V e T:V→W” ove il codominio di S coincide con il dominio di T definendo così una nuova applicazione, ancora una volta lineare (trovi le definizioni ai “link correlati” indicati in basso), che corrisponde alla composizione di S con T, che si scrive “T o S” e si legge “T composto S” (nel caso specifico “T o S: U→W”). Qualora U, V, W siano uguali, ciò significa che T ed S sono endomorfismi (trovi le definizioni ai “link correlati” indicati in basso) pertanto, in questo caso, risultano definiti sia “T o S” che “S o T” ma in generale la composizione non è commutativa ovvero T o S ≠ S o T.
Un curioso esempio
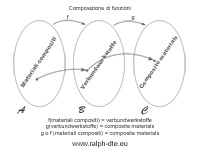
Se però il concetto dovesse essere inizialmente difficile da immaginare si può porre all’attenzione un esempio banale come quello che segue: immaginate di dover tradurre in una lingua che non conoscete il termine “materiali compositi”, ipotiziamo che questa lingua sia il tedesco e che per la traduzione adoperiate un traduttore online come ad esempio il traduttore di Google. Traducendo dall’italiano al tedesco il termine “materiali compositi” otterrete “verbundwerkstoffe”. Ora però non avete idea se il termine ottenuto è realmente quello che desiderate oppure un sinonimo o un termine con un significato adatto ad altri contesti. Così, per una verifica, potete ad esempio tradurre il termine tedesco nel suo corrispondente in un’altra lingua che conoscete, ad esempio l’inglese. Se il risultato della traduzione dal tedesco all’inglese, del termine “verbundwerkstoffe”, è “composite materials”, avrete la conferma che anche la traduzione dall’italiano al tedesco è corretta. Non avete fatto altro che comporre due funzioni.
ITA: materiali compositi (o compositi)
ENG: composite materials (o composites)
GER: verbundwerkstoffe
f: funzione dal termine italiano al termine tedesco
f(materiali compositi) = verbundwerkstoffe
g: funzione dal termine tedesco al termine inglese
g(verbundwerkstoffe) = composite materials
g o f: composizione di f con g
g o f(materiali compositi) = composite materials
Link correlati
Introduzione al concetto di funzione matematica
Dominio, codominio, invertibilità, monotonia
Funzione (applicazione), iniettività, suriettività, linearità
Endomorfismo, isomorfismo, monomorfismo, epimorfismo