Rubrica: Officina della Matematica
Titolo o argomento: Coordinate polari
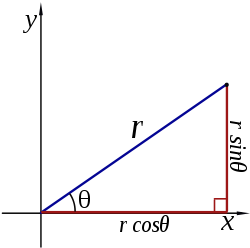
Coordinate polari: le due coordinate, in genere indicate con (r,θ) o con (ρ,θ), che individuano un punto nel piano mediante la lunghezza “r” del segmento (modulo) che unisce il punto all’origine (o polo) e l’angolo “θ” (argomento) formato da tale segmento con un asse prefissato. Le coordinate polari suddividono il vettore in una componente scalare, il modulo, e in una componente di rotazione, l’argomento.
Le coordinate polari del punto di coordinate (ρ,θ) sono:
(x,y) = (ρ·cosθ, ρ·sinθ)
Prodotto in coordinate polari
Il prodotto in coordinate polari tra v1 = (x1, y1) e v2 = (x2, y2) si calcola (ovviamente tenendo conto del fatto che (x,y) = (ρ·cosθ, ρ·sinθ) ) come segue: v1 · v2 = ρ1ρ2 (cos(θ1+θ2), sin(θ1+θ2)) e sviluppato con le opportune formule goniometriche di addizione e sottrazione del seno e del coseno.
Prodotto in coordinate cartesiane
L’equivalente del prodotto in coordinate polari, in coordinate cartesiane, si scrive come segue: (x1, y1) · (x2, y2) = (x1x2 – y1y2, x1y2 + x2y1) che altro non è che il prodotto che si adotta con i numeri complessi (vedi gli articoli: Numeri complessi, Numeri complessi – parte seconda).