Rubrica: Officina della Matematica
Titolo o argomento: I numeri complessi – parte seconda
Nell’articolo “Numeri complessi” abbiamo introdotto in modo banale l’utilità di questa tipologia di numeri, ora complicheremo leggermente le cose al fine di introdurre concetti un po’ più approfonditi. Su Rn (con n≥3) non è possibile definire un prodotto che, assieme alla somma usuale, lo renda un campo (vedi l’articolo: “Assiomi campo ed assiomi spazio vettoriale“). Su R2 invece ciò è possibile tramite il campo C dei numeri complessi. E’ importante ricordare che ogni numero complesso non nullo possiede esattamente n radici n-esime distinte, questo significa che un polinomio di grado n, su C, ammette sempre esattamente n radici, cosa che non accade sempre su R (vedi il Teorema fondamentale dell’algebra). Introduciamo di seguito alcune definizioni utili.
Premessa
Modulo (o norma) ρ del vettore v
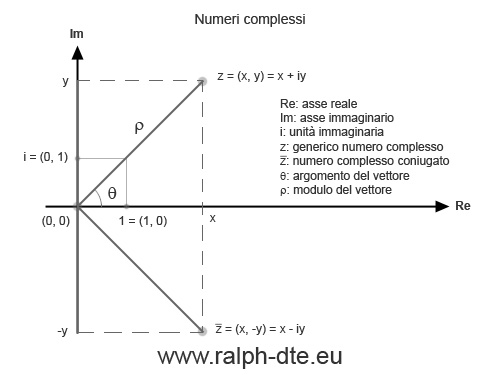
Se v=(x,y) appartenente ad R2 è un vettore non nullo applicato nell’origine, il suo modulo o norma (ovvero la sua lunghezza) è il numero positivo: ρ=|v|=√(x2+y2). Attenzione perchè su alcuni testi trovate il modulo ed il valore assoluto espressi con il medesimo simbolo, mentre su altri testi trovate il valore assoluto espresso come segue |x| ed il modulo (o norma) espresso con la doppia barretta ||v||.
Argomento θ del vettore v
Si tratta di quell’angolo θ appartenente a [0, 2π) che viene misurato in radianti e per il quale x = ρcosθ e y = ρsinθ (vedi l’articolo: “Coordinate polari“).
Prodotto in coordinate polari e coordinate cartesiane
Vedi l’articolo: “Coordinate polari“.
I numeri complessi
Come si descrive un numero complesso
Il numero complesso “z” si descrive come segue “z = x+iy” dove “x” è la parte reale (Re z) e “y” è il coefficiente (numero reale) della parte immaginaria “iy” (Im z) di “z”. La lettera “i” rappresenta invece l’unità immaginaria. Spesso trovate il numero complesso “z” descritto come segue “z = a+ib”, ovviamente è la medesima cosa. Vale la pena osservare che:
a+i0 è un numero reale
0+ib è un numero immaginario puro
a+ib è un generico numero complesso
In numeri
z = √-1 non è altro che il numero complesso “i” ovvero l’unità immaginaria i = √-1, per definizione: i2 = -1 e, per analogia con i numeri reali, -i2 = -1 mentre -(i)2=+1 (attenzione alle parentesi). Ad esempio √-16 non è altro che √-1 · √16, ovvero i√16 e quindi 4i.
i·(-i) = 1
± i2 = -1
i3 = i2 · i = -i
i4 = i2 · i2 = 1
x2+1=0 ovvero x2=-1 ha come radici (soluzioni) x1=i e x2=-i che, dimostrazione banale, al quadrato danno entrambi il valore “-1”.
Per la cronaca, anche se si tratta di un concetto che va approfondito, riportiamo il valore della radice di i: √i = ±(1+i)/√2, infatti, elevando al quadrato il risultato otteniamo (ovviamente): [±(1+i)/√2]² = (1+i)²/2 = (1+i²+2i)/2 = (1-1+2i)/2 = i
Numero complesso immaginario puro
Quando la parte reale Re(z) = 0, ovvero a = 0, il numero immaginario z = ib si dice immaginario puro.
Complesso coniugato e coniugio
Il complesso coniugato di un numero complesso “z = a+ib” è il numero complesso z* = a-ib. L’applicazione che associa ad un numero complesso il suo coniugato si chiama coniugio.
La base canonica di C su R
Il campo C è uno spazio vettoriale di dimensione 2 su R, una sorta di R2 sotto altre vesti. La base canonica di C su R è data da [(1,0), (0,1)].
Unità moltiplicativa 1
Il vettore (1,0) della base canonica riportata al punto precedente è detto unità moltiplicativa di C e viene indicato semplicemente con 1.
Unità immaginaria i
Il vettore (0,1) della base canonica riportata poco sopra è detto unità immaginaria e viene indicato con i. Il prodotto i · i = i2 = (0,1) · (0,1) = (-1, 0) = -1 (vedi il prodotto di due numeri complessi di seguito).
Somma di due numeri complessi
(a,b) + (c,d) = (a+c, b+d) per esempio i + i = (0, 1) + (0, 1) = (0+0, 1+1) = (0, 2)
Prodotto di due numeri complessi
(a,b) (c,d) = (ac-bd, bc+ad) per esempio i · i = (0, 1) · (0, 1) = (0 – 1, 0+0) = (-1, 0) = -1
Inverso di un numero complesso
1/(a+ib) = (a-ib)/((a+ib)·(a-ib)) = (a-ib)/(a2+b2) ovvero l’inverso di “z” è uguale al rapporto tra il “coniugato di z” (vedi la voce “complesso coniugato e coniugio” riportata precedentemente) e il “prodotto del numero complesso z per il suo coniugato” (ovvero il quadrato del suo modulo). Quindi 1/z = z*/z·z* = z*/|z|2. Per ottenere l’inverso di z, come nell’esempio all’inizio di questo paragrafo, è sufficiente moltiplicare e dividere, per a-ib, la quantità 1/(a+ib) ed eseguire le normali operazioni.
Inverso di “i”: 1/i = -i/1 dove “-i” è il complesso coniugato di “i” ed il numero 1 presente al “denominatore” è il quadrato del modulo di z = a+ib (in questo caso z=0+i1 ovvero z=i). Quindi l’inverso di “i” vale “-i”.
Il quadrato di un numero complesso
(a+ib)2 = (a+ib) · (a+ib) = (a2-b2) + i(2ab) il tutto calcolato normalmente membro a membro facendo attenzione al fatto che ib·ib vale -b2 in quanto i2 = -1 (spesso le prime volte si tende a non ricordarlo).
Modulo di un numero complesso
Il modulo di “z” è il numero reale |z| = √(x2+y2) oppure, se volete |z| = √(a2+b2), ovviamente è la stessa cosa. Il modulo non è altro che la distanza del generico punto P dall’origine, in questo caso il punto P viene rappresentato sul piano complesso o piano di Gauss. E’ utile notare che il modulo di “z” è uguale al modulo del suo complesso coniugato “z*”.
Il quadrato del modulo di un numero complesso
Moltiplicando “z = a+ib” per il suo coniugato “z* = a-ib” si ottiene a2+b2 che altro non è che il quadrato del modulo di z e quindi il quadrato di |z| = √(a2+b2). Ovviamente per modulo non si intende il valore assoluto, bensì la lunghezza, l’intensità di un vettore.
Scrittura di un generico numero complesso
Come abbiamo visto la base canonica di C su R è [(1,0), (0,1)] dove (1,0) si può scrivere semplicemente “1” e (0,1) non è altro che “i”, pertanto la base canonica di C su R può essere scritta come segue: (1, i). Questo ci permette di scrivere comodamente un generico numero complesso (a, b) come segue: (a, b) = (a, 0) + (0, b) = a(1, 0) + b(0, 1) = a · 1 + b · i = a + ib. Ricorda che per effettuare le normali operazioni troverai il numero complesso scritto nella forma z = x+iy mentre per la rappresentazione sul piano complesso o piano di Gauss sarà semplicemente (x, y).
“i” scritto in coordinate cartesiane e polari
Abbiamo detto, al paragrafo inerente l’unità immaginaria, che il vettore (0,1) della base canonica di C è detto unità immaginaria e viene indicato con “i”. In coordinate polari “i” ha un modulo e un argomento e, più precisamente, ha modulo 1 e argomento π/2, ovvero (1, π/2).
Un numero complesso può essere scritto in forma trigonometrica e, da z = x+iy, diventa z = ρcosθ + i ρsinθ in quanto, come abbiamo visto nella premessa, x = ρcosθ e y = ρsinθ. Da ciò è possibile notare che x2+y2 = ρ2cos2θ + ρ2sin2θ = ρ2 (cos2θ + sin2θ) = ρ2 · 1 (per via dell’equazione fondamentale della trigonometria). Da ρ2 = x2+y2 ritroviamo ρ=|v|=√(x2+y2) ovvero il modulo (e tutto torna).
Radice (o zero)
Se “z” è un numero complesso qualsiasi (diverso da 0) ed “n” è un numero qualunque maggiore di zero, allora la radice ennesima di “z” (n√z) è il numero complesso (se esiste) “w” tale che “wn = z” e quindi “n√z = w”. Questo significa che l’equazione nell’incognita “w” descritta da “wn = z” ha esattamente “n” soluzioni.
Teorema fondamentale dell’algebra
Esso afferma che un’equazione del tipo a0xn + a1xn-1 + … + an = 0, dove a0, a1, an sono dei numeri complessi qualsiasi, ha sempre esattamente n radici (vedi il paragrafo precedente).
Molteplicità
Le radici (vedi i due paragrafi precedenti) devono essere contate con la loro molteplicità… cosa vuol dire? Se abbiamo un polinomio, nella variabile z, a coefficienti complessi e se z0 è una sua radice (o zero, o soluzione), allora possiamo dire che z0 è una radice di molteplicità “m” (appartenente ai numeri naturali) se il polinomio dato è divisibile per il polinomio (z – z0)m ma non è divisibile per il polinomio (z – z0)m+1.
Ad esempio il polinomio p(z) = (z-i)2·(z+i) ha radici “z01 = i” e “z02 = -1″ pertanto se divido il polinomio per (z-z0)m e quindi, nel caso della prima radice, per (z-i)m mi accorgo che al massimo la molteplicità m può valere 2, quindi la radice “i” ha molteplicità 2. Se eseguo la stessa operazione con la seconda radice, ovvero con “-1”, mi accorgo che la m può valere al massimo 1, quindi la radice -1 ha molteplicità 1.