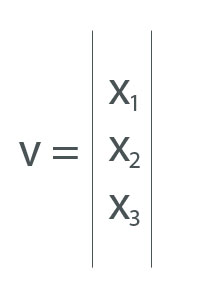Rubrica: Fisicamente
Titolo o argomento: Vista 3D di un vettore
Se l’immagine presente nell’articolo “Cos’è un vettore” non vi era chiara, ecco a voi la vista in 3d (animazione sotto) di un vettore che segnala lo spostamento dall’origine degli assi O=(0, 0, 0) al punto A=(1, 4, 2)
https://www.ralph-dte.eu/gallery/scienze/matematicamente/vettori/vettore_3d.swf
In pratica in uno spostamento un vettore non fa altro che indicare quanto ci si è mossi lungo l’asse x, lungo l’asse y e lungo l’asse z, rispetto ad un sistema di assi cartesiani di riferimento.
Credo e spero che più chiaro di così non sia possibile. Cerchiamo di rendere gli articoli della nostra rubrica più brevi e chiari possibile. Ci rendiamo conto che aprire la pagina di un sito che si interessa di matematica e trovarla piena di formule fitte fitte scritte piccolo piccolo, non sia il modo migliore per tentare di capire agevolmente ciò che il libro che utilizzate ha spiegato troppo velocemente ad esempio.
Continuo a ricordare che un’applicazione molto gradita ai giovani circa i vettori, è senza dubbio quella citata nell’articolo che fa riferimento alla simulazione di corse automobilistiche. In tale articolo potete capire l’importanza fondamentale della conoscenza dei vettori in modo concreto.