matrice minore | Ralph DTE

Rubrica: Officina della Matematica

Titolo o argomento: Metodi e note per il calcolo del determinante
Matrici quadrate
Che cos’è il determinante?

La definizione più banale: Il determinante è un’operazione che associa un numero a tutte le matrici quadrate. La definizione con più connessioni: Il determinante è una funzione che ci indica esattamente quando n vettori di Rⁿ sono linearmente indipendenti, infatti se due righe (o colonne) di una matrice quadrata sono proporzionali (e quindi linearmente dipendenti) il determinante vale zero. Ciò è strettamente legato al concetto di rango di una matrice (ovvero il numero dei vettori linearmente indipendenti) ed al fatto di cercare la dimensione della sottomatrice più grande con determinante diverso da zero in modo da stabilire la dimensione dell’immagine di un’applicazione lineare. Il determinante è omogeneo e additivo in ogni riga, da ciò si deduce che il determinante è lineare.

Prima di effettuare conti inutili

Se una riga (o colonna) di una matrice contiene tutti zeri, allora il determinante vale zero.
Se due righe (o colonne) di una matrice quadrata sono uguali allora il determinante vale zero.
Se due righe (o colonne) di una matrice quadrata sono proporzionali allora il determinante vale zero.
Se la matrice è diagonale il determinante si calcola moltiplicando tra loro gli elementi della diagonale.
Se la matrice è triangolare il determinante si calcola moltiplicando tra loro gli elementi della diagonale.
Il determinante della matrice identità vale 1.

Altre proprietà importanti
Se si scambiano due righe il determinante cambia di segno.
Se ad una riga sommo un’altra riga moltiplicata per uno scalare ≠ 0 il determinante non cambia.
Se ad una colonna sommo un’altra colonna moltiplicata per uno scalare ≠ 0 il determinante non cambia.
Se si moltiplicano gli elementi di una riga per uno scalare k anche il determinante risulta moltiplicato per k.
Se una matrice viene trasposta il determinante rimane il medesimo.
Date due matrici quadrate dello stesso ordine, la matrice prodotto ha per determinante il prodotto dei determinanti delle singole matrici.
Determinante di matrici del primo, secondo e terzo ordine

Premesso che il determinante di una matrice A del primo ordine 1 x 1 è uguale al numero stesso che compare nella matrice, passiamo subito al metodo relativo alle matrici del secondo ordine 2 x 2 nelle quali il determinante è uguale alla differenza fra il prodotto dei due elementi della diagonale principale e il prodotto fra i due elementi della diagonale secondaria.

Determinante di una matrice del secondo ordine

Il determinante di una matrice A del terzo ordine 3 x 3 è uguale alla somma dei prodotti di una riga qualunque per i rispettivi complementi algebrici. Cosa sono i complementi algebrici? Come si calcolano? Vedi il paragrafo successivo.

Determinante di una matrice del terzo ordine

Sopra, la formula di risoluzione delle matrici 3 x3, dove a₁₁, a₁₂, a₁₃ sono ovviamente gli elementi della prima riga della matrice 3 x 3, mentre A₁₁, A₁₂, A₁₃ sono i complementi algebrici dei rispettivi elementi. Nota che, se anche nella formula appena citata compaiono tutti segni positivi, in realtà il complemento algebrico di un elemento, la cui somma degli indici è pari, deve essere preceduto dal segno + (es. A₁₁); mentre il complemento algebrico di un elemento, la cui somma degli indici è dispari, deve essere preceduto dal segno – (es. A₁₂). Ovviamente se vi è una riga che contiene uno o più zeri la si sceglie al fine di ridurre notevolmente i calcoli.

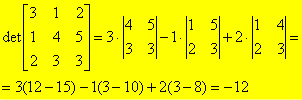
Complemento algebrico ovvero determinante della matrice 2x2 ottenuta dalla matrice 3x3 cancellando 1 riga e una colonna

Complemento algebrico (o determinante della matrice minore)

Il complemento algebrico di un elemento “a_ij” di una matrice A di ordine 3 è il determinante della matrice di ordine 2 (detta matrice minore) ottenuta da A sopprimendo la riga “i” e la colonna “j” cui l’elemento appartiene. Il complemento algebrico deve essere preceduto dal segno + o dal segno – a seconda che l’elemento “a_ij” sia di classe pari (cioè la somma degli indici dà un numero pari) o classe dispari (cioè la somma degli indici dà un numero dispari).

Calcolo del determinante di una matrice del terzo ordine

Quindi il determinante di una matrice del terzo ordine 3 x3 si definisce mediante determinanti del secondo ordine, estratti dalla matrice stessa, ovvero i complementi algebrici. Dalla matrice 3 x 3 si cancella una riga e una colonna e si calcola il determinante (come nel caso del secondo ordine) della matrice 2 x 2 dei termini restanti.

Metodo Sarrus per le matrici del terzo ordine

Il determinante di una matrice 3 x 3 (vedi ad esempio il caso precedente) può essere calcolato anche in un altro modo utilizzando la regola di Sarrus.

Per il calcolo del determinante si riscrivono, alla destra della matrice, le prime due colonne della matrice stessa.
Si moltiplicano poi i termini lungo la diagonale principale e lungo le due diagonali (solo quelle con tre termini) parallele ad essa, dopodichè si scrivono i prodotti ottenuti e si sommano tra loro.
Il procedimento viene ripetuto moltiplicando e poi sommando (come nel punto precedente) i termini lungo la diagonale secondaria e lungo le due diagonali (sono quelle con tre termini) parallele ad essa.
Il determinante sarà uguale alla differenza fra la prima e la seconda somma di prodotti.

Calcolo dei determinanti di matrici di ordine superiore al terzo

Calcolare il determinante di una matrice n x n consiste essenzialmente nell’applicazione ripetuta delle regolette sopra trattate; se abbiamo ad esempio una matrice 4 x 4 possiamo adoperare la formula che fa uso del complemento algebrico e, per semplificare le operazioni, risolvere le matrici minori 3 x 3 ottenute con la regola di Sarrus.

Calcolo del determinante mediante eliminazione di Gauss

Se S è una matrice triangolare superiore ottenuta dalla matrice A effettuando un’eliminazione di Gauss (o una riduzione a scala) con “σ scambi di righe”, allora il determinante della matrice A si ricava mediante la formula:

dove il numero (-1)^σ è uguale a “-1” se σ è dispari, ed è uguale a “+1” se σ è pari.

In sostanza il determinante in questo caso lo si ottiene moltiplicando tra loro gli elementi della diagonale principale (ovvero i pivot p1, p2, …, pn, dato che si tratta di una matrice triangolare ottenuta mediante eliminazione di Gauss) e inserendo il segno corretto che tiene conto di quanti scambi di righe sono stati effettuati.

Sviluppo di Laplace

Il determinante di una matrice quadrata A è uguale alla somma dei prodotti degli elementi di una riga qualsiasi per i rispettivi complementi algebrici. Si tratta del metodo che, forse più semplicemente, abbiamo riportato in linea generale, pochi paragrafi più su, occupandoci delle matrici del terzo ordine. Lo sviluppo di Laplace può essere effettuato lungo la colonna j-esima così come lungo la riga i-esima.

Un esempio numerico è sempre gradito, osserviamo la seguente matrice 5 x 5:
Esempio sviluppo di Laplace su matrice 5 x 5

Scegliamo di eseguire il calcolo lungo la terza colonna in quanto presenta tutti zeri ad eccezione dell’elemento “a₅₃” che invece vale 1. Andiamo pertanto ad eseguire i calcoli solo sull’elemento “a₅₃” ed otteniamo quindi:

Esempio sviluppo di Laplace su matrice 5 x 5

Ora il gioco si ripete, si tratta infatti di un procedimento ricorsivo che si ripete tante più volte quanto maggiore è l’ordine della matrice. Trovandoci ora davanti ad una matrice 4 x 4 di cui si deve ricavare il determinante, si riapplica il medesimo procedimento, si sceglie ad esempio di eseguire i calcoli lungo la prima colonna dove, nuovamente, troviamo tutti zeri ad eccezione dell’elemento “a₂₁” che vale 1.

Esempio sviluppo di Laplace su matrice 4 x 4

A questo punto possiamo scegliere se risolvere la matrice 3 x 3 utilizzando nuovamente lo sviluppo di Laplace, oppure adottando la regola di Sarrus. Scegliendo la seconda opzione si ricava il determinante di A che vale -27.

Matrici rettangolari
Caratteristica di una matrice m x n

Premesso che non è possibile (non è logico) calcolare il determinante di una matrice m x n (dato che ci si trova davanti ad un numero di equazioni differente dal numero di incognite) è però opportuno definire il concetto di caratteristica di una matrice m x n.

Se si considera una matrice 3 x 4 è possibile estrarre da essa delle sottomatrici 3 x 3 il cui determinante si chiamerà “minore di ordine 3”. E’ possibile anche estrarre delle matrici 2 x 2 e, in tal caso, il loro determinante si chiamerà “minore di ordine 2”. Quindi, generalizzando, il minore di ordine q di una matrice m x n sarà il determinante della sottomatrice quadrata estratta dalla matrice iniziale ed avente q righe e q colonne.

La caratteristica di una matrice non nulla sarà quindi il massimo ordine dei minori non nulli estraibili da essa.

Note

Matrice minore: la matrice che si ricava eliminando la “riga i” e la “colonna j” relative all’elemento “a_ij“.
Minore complementare: determinante della matrice minore.
Complemento algebrico (o cofattore): lo scalare ottenibile dal minore complementare di “a_ij” preso con il proprio segno o con il segno cambiato a seconda che la somma i+j sia rispettivamente pari o dispari.

Suggerimenti per la rapidità di calcolo

Nel caso di matrici con molti zeri, dette anche matrici “sparse”, risulta conveniente eseguire il calcolo del determinante tramite gli sviluppi di Laplace. Nel caso invece di matrici senza particolari caratteristiche può risultare di gran lunga meno laborioso il metodo che si basa sull’eliminazione di Gauss.

Link correlati
Introduzione alle matrici

Rubrica: Officina della Matematica

Titolo o argomento: Introduzione alle matrici

L’articolo che segue “ovviamente” non sostituisce le importanti nozioni riportate in un ottimo libro, quanto riportato ha il solo ed unico scopo di fungere da memorandum di rapida esplorazione. Spetta poi al lettore approfondire debitamente i concetti di cui necessita. Innanzitutto ricordiamo che:

con M_m,n si intende l’insieme delle matrici con m righe ed n colonne
con M_m,n(R) si intende l’insieme delle matrici a coefficienti Reali
con M_m,n(C) si intende l’insieme delle matrici a coefficienti complessi
con Aⁿ si intende la colonna n-esima della matrice M_m,n
con A_m si intende la riga m-esima della matrice M_m,n
con GL_n si intende l’insieme delle matrici invertibli di ordine n
con I_n si intende la matrice identità (o se vogliamo identica o, ancora, unità)
con A^T si intende la matrice trasposta
con A^H si intende la matrice trasposta coniugata

Una matrice è una tabella rettangolare di numeri con “m” righe ed “n” colonne. Il numero “a_ij” è l’elemento posizionato alla riga “i” in corrispondenza della colonna “j”. Una matrice è un importante strumento matematico che concretizza la complessa teoria matematica ed è ampiamente utilizzato in diverse branche dell’ingegneria.

Una matrice quadrata è una matrice che ha tante righe quante colonne. Una matrice quadrata “n x n” è detta di ordine n. Una matrice quadrata può essere “semplificata” e trasformata in una matrice triangolare superiore grazie ai procedimenti previsti dall’eliminazione di Gauss.

Una matrice quadrata diagonale è una matrice che ha tutti gli elementi nulli eccetto quelli presenti sulla diagonale principale ovvero la diagonale che va dall’angolo in alto a sinistra a quello in basso a destra.

Una matrice simmetica è una matrice quadrata A a coefficienti reali tale per cui la sua trasposta A^T è uguale alla matrice iniziale, ovvero A = A^T.

Una matrice antisimmetrica è una matrice quadrata A a coefficienti reali tale per cui: A^T = -A.

Una matrice identica è una matrice che ha sulla diagonale princiapali tutti valori pari a 1 e sulle restanti posizioni tutti valori pari a 0.

Una matrice completa è una matrice che al suo interno comprende la matrice dei coefficienti e la matrice dei termini noti.

Una matrice triangolare superiore è caratterizzata dall’avere tutti gli elementi al di sotto della diagonale principale sono nulli; viceversa si definisce matrice triangolare inferiore.

Una matrice quadrata singolare ha almeno uno dei suoi pivot nullo, mentre una matrice quadrata non singolare ha tutti i pivot non nulli.

Una matrice a scala è una matrice “m x n” i cui pivot (posizionati a scala) sono tutti non nulli. Matrici qualunque possono essere semplificate tramite riduzione a scala, ovvero tramite un procedimento simile all’eliminazione di Gauss.

Una matrice trasposta è una matrice in cui vengono scambiate le righe con le colonne. La prima riga diventa la prima colonna, la seconda riga diventa la seconda colonna e così via. La matrice trasposta della matrice A si indica con A^T.

La matrice coniugata di A è la matrice Ã appartenente all’insieme delle matrici a coefficienti complessi, ovvero a M_m,n(C), i cui elementi sono i “coniugati” degli elementi di A. Per sapere cosa sono gli elementi coniugati è necessario studiare i numeri complessi (potrebbe interessarti leggere gli articoli: I numeri complessi – I numeri complessi parte seconda).

La matrice trasposta coniugata (o aggiunta) A^H (appartenente all’insieme delle matrici a coefficienti complessi) di A è la matrice trasposta della coniugata di A. La matrice A viene detta hermitiana quando A = A^H, mentre viene detta anti-hermitiana quando A^H = -A.

Una matrice invertibile è una matrice A appartenente a M_m,n(K) per la quale esiste una matrice B appartenente a M_m,n(K) tale che A·B = B·A = I_n (dove I_n sta per matrice identica). La matrice B, inversa di A, è unica e si indica con A^-1. L’insieme delle matrici invertibili di ordine n si rappresenta con GL_n.

Una matrice di cambiamento di base (o matrice di cambiamento di coordinate) è una matrice di passaggio dalla base B alla base B’, tale matrice si indica con B. La matrice di cambiamento di base B contiene per colonne le coordinate dei vettori della nuova base B’ rispetto alla vecchia base B. La matrice di cambiamento di base B^-1 è ovviamente la matrice di passaggio dalla base B’ alla base B (direzione inversa alla precedente), essa contiene per colonne le coordinate dei vettori della base B rispetto alla base B’.

Una matrice associata all’applicazione lineare T… – In preparazione

Le matrici quadrate simili A e A’ sono tali solo se esiste una matrice B invertibile tale per cui è valida la relazione: A’ = B^-1AB.

La matrice minore (o minore complementare) è la matrice che si ottiene cancellando la riga i e la colonna j di una matrice quadrata durante il calcolo del determinante. La matrice minore si indica con A_ij dove “i” e “j” indicano rispettivamente la riga e la colonna che sono state eliminate per il calcolo del determinante (es. A₁₃ se è stata cancellata la riga 1 e la colonna 3).

Link correlati

Metodi per calcolare il determinante di una matrice