Rubrica: Officina della Matematica
Titolo o argomento: Gradiente di uno scalare
Sia “p” uno scalare (ad esempio la pressione o la temperatura) e sia V = (V1, V2, V3) un vettore (ad esempio un vettore velocità). Siano entrambi funzione del punto (x1, x2, x3) o se vogliamo del punto (x, y, z), è la stessa cosa. Il gradiente di uno scalare è il seguente vettore:
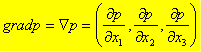
Il simbolo 
è l’operatore differenziale vettoriale Nabla e lo scalare “p” è detto”Potenziale del risultante campo vettoriale”. E’ anche possibile definire il gradiente di un vettore (gradV) applicando la definizione nella formula sopra ad ogni componente. Il risultato che si ottiene è il seguente (gradV1, gradV2, gradV3) ed è un vettore di vettori.